
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 562 Атанасян — Подробные Ответы
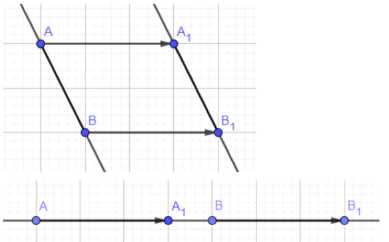
Известно, что \(АА_1 = ВВ_1\). Как расположены по отношению друг к другу: а) прямые \(АВ\) и \(A_1B_1\); б) прямая \(АВ\) и плоскость, проходящая через точки \(А_1\) и \(В_1\); в) плоскости, одна из которых проходит через точки \(А\) и \(В\), а другая проходит через точки \(А_1\) и \(В_1\)?
а) Прямые \(АВ\) и \(A_1B_1\) параллельны или совпадают. б) Прямая \(АВ\) параллельна плоскости, проходящей через \(A_1B_1\), или лежит в ней. в) Плоскости, проходящие через \(АВ\) и \(A_1B_1\), параллельны, пересекаются или совпадают.
Дано, что \( \vec{AA_1} = \vec{BB_1} \). Это означает, что вектор, направленный из точки \(A\) в точку \(A_1\), равен вектору, направленному из точки \(B\) в точку \(B_1\).
а) Рассмотрим взаимное расположение прямых \(АВ\) и \(A_1B_1\). Из равенства векторов \( \vec{AA_1} = \vec{BB_1} \) следует, что четырехугольник \(ABB_1A_1\) является параллелограммом. В параллелограмме противоположные стороны параллельны. Следовательно, прямая \(АВ\) параллельна прямой \(A_1B_1\). Возможен также вырожденный случай параллелограмма, когда точки \(А, В, В_1, А_1\) лежат на одной прямой. В этом случае прямые \(АВ\) и \(A_1B_1\) совпадают. Таким образом, прямые \(АВ\) и \(A_1B_1\) параллельны или совпадают.
б) Рассмотрим взаимное расположение прямой \(АВ\) и плоскости, проходящей через точки \(А_1\) и \(В_1\). Плоскость проходит через прямую \(A_1B_1\). Из пункта а) мы установили, что прямая \(АВ\) параллельна прямой \(A_1B_1\) или совпадает с ней. Если прямая \(АВ\) параллельна прямой \(A_1B_1\) и не совпадает с ней, то прямая \(АВ\) параллельна прямой, лежащей в плоскости, и сама не лежит в этой плоскости. Следовательно, прямая \(АВ\) параллельна плоскости, проходящей через \(A_1B_1\). Если прямая \(АВ\) совпадает с прямой \(A_1B_1\), то прямая \(АВ\) лежит в плоскости, проходящей через \(A_1B_1\), поскольку прямая \(A_1B_1\) лежит в этой плоскости. Таким образом, прямая \(АВ\) параллельна плоскости, проходящей через \(A_1B_1\), или лежит в ней.
в) Рассмотрим взаимное расположение плоскостей, одна из которых проходит через прямую \(АВ\), а другая проходит через прямую \(A_1B_1\). Из пункта а) мы знаем, что прямые \(АВ\) и \(A_1B_1\) параллельны или совпадают. Если прямые \(АВ\) и \(A_1B_1\) параллельны и различны, то плоскости, проходящие через эти параллельные прямые, могут быть параллельны (если они не совпадают) или пересекаться. Если прямые \(АВ\) и \(A_1B_1\) совпадают, то плоскости, проходящие через эту общую прямую, могут совпадать или пересекаться по этой прямой. Следовательно, плоскости, проходящие через \(АВ\) и \(A_1B_1\), могут быть параллельны, пересекаться или совпадать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!