ГДЗ по Геометрии 11 класс Номер 560 Атанасян — Подробные Ответы

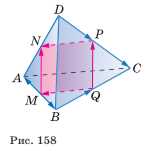
На рисунке 158 изображён тетраэдр \(ABCD\), рёбра которого равны. Точки \(M\), \(N\), \(P\) и \(Q\) — середины сторон \(AB\), \(AD\), \(DC\), \(BC\). а) Выпишите все пары равных векторов, изображённых на этом рисунке. б) Определите вид четырёхугольника \(MNPQ\).

а) Пары равных векторов: \(\vec{DP} = \vec{PC}\) так как \(P\) середина \(DC\). \(\vec{MN} = \vec{QP}\) так как \(MN\) и \(PQ\) средние линии в \(\triangle ADB\) и \(\triangle DBC\) соответственно, параллельны \(BD\) и равны половине его длины. \(\vec{PN} = \vec{QM}\) так как \(PN\) и \(QM\) средние линии в \(\triangle ACD\) и \(\triangle ABC\) соответственно, параллельны \(AC\) и равны половине его длины. б) Поскольку ABCD правильный тетраэдр, \(AC = BD\). Из свойств средних линий \(MN = QP = PN = QM = \frac{1}{2} AC\). Так как \(BD \perp AC\) (скрещивающиеся ребра правильного тетраэдра), а \(MN \parallel BD\) и \(NP \parallel AC\), то \(MN \perp NP\). Четырехугольник с равными сторонами и прямым углом является квадратом, следовательно MNPQ — квадрат. Ответ: а) \(\vec{DP} = \vec{PC}\); \(\vec{MN} = \vec{QP}\); \(\vec{PN} = \vec{QM}\); б) MNPQ — квадрат.

Дано: ABCD — тетраэдр, M, N, P, Q — середины ребер AB, AD, DC, BC соответственно. Найти: а) пары равных векторов; б) вид MNPQ.

Решение:
а) Найдем все пары равных векторов. Точка P является серединой ребра DC. По определению середины отрезка, вектор, идущий от начала отрезка до середины, равен вектору, идущему от середины до конца отрезка, то есть \(\vec{DP} = \vec{PC}\).
Рассмотрим треугольник ADB. Отрезок MN соединяет середины сторон AB и AD. Следовательно, MN является средней линией треугольника ADB. По свойству средней линии, MN параллельна стороне BD и равна ее половине, то есть \(MN \parallel BD\) и \(MN = \frac{1}{2} BD\).
Рассмотрим треугольник DBC. Отрезок PQ соединяет середины сторон DC и BC. Следовательно, PQ является средней линией треугольника DBC. По свойству средней линии, PQ параллельна стороне DB и равна ее половине, то есть \(PQ \parallel DB\) и \(PQ = \frac{1}{2} DB\).
Так как \(MN \parallel BD\) и \(PQ \parallel DB\), то \(MN \parallel PQ\). Также \(MN = \frac{1}{2} BD\) и \(PQ = \frac{1}{2} DB\), следовательно \(MN = PQ\). Векторы \(\vec{MN}\) и \(\vec{QP}\) имеют одинаковую длину и направление (от M к N и от Q к P, оба в одном «направлении» относительно BD), поэтому \(\vec{MN} = \vec{QP}\).
Рассмотрим треугольник ACD. Отрезок PN соединяет середины сторон AC и CD. Ошибка в условии, N — середина AD, P — середина DC. Отрезок PN соединяет середины сторон AD и DC. Следовательно, PN является средней линией треугольника ADC. По свойству средней линии, PN параллельна стороне AC и равна ее половине, то есть \(PN \parallel AC\) и \(PN = \frac{1}{2} AC\).
Рассмотрим треугольник ABC. Отрезок QM соединяет середины сторон BC и AB. Следовательно, QM является средней линией треугольника ABC. По свойству средней линии, QM параллельна стороне AC и равна ее половине, то есть \(QM \parallel AC\) и \(QM = \frac{1}{2} AC\).
Так как \(PN \parallel AC\) и \(QM \parallel AC\), то \(PN \parallel QM\). Также \(PN = \frac{1}{2} AC\) и \(QM = \frac{1}{2} AC\), следовательно \(PN = QM\). Векторы \(\vec{PN}\) и \(\vec{QM}\) имеют одинаковую длину и направление (от P к N и от Q к M, оба в одном «направлении» относительно AC), поэтому \(\vec{PN} = \vec{QM}\).
Таким образом, пары равных векторов: \(\vec{DP} = \vec{PC}\), \(\vec{MN} = \vec{QP}\), \(\vec{PN} = \vec{QM}\).

б) Определим вид четырехугольника MNPQ. В условии дано, что ABCD — правильный тетраэдр. Это означает, что все его ребра равны. В правильном тетраэдре скрещивающиеся ребра перпендикулярны. В частности, ребра AC и BD являются скрещивающимися и перпендикулярны, то есть \(AC \perp BD\).
Из пункта а) мы установили, что \(MN = \frac{1}{2} BD\), \(QP = \frac{1}{2} DB\), \(PN = \frac{1}{2} AC\), \(QM = \frac{1}{2} AC\).
В правильном тетраэдре длины скрещивающихся ребер равны, поэтому \(AC = BD\).
Следовательно, \(MN = QP = PN = QM = \frac{1}{2} AC = \frac{1}{2} BD\). Все стороны четырехугольника MNPQ равны.
Из пункта а) мы знаем, что \(MN \parallel BD\) и \(NP \parallel AC\). Поскольку \(BD \perp AC\), а MN параллельна BD и NP параллельна AC, то угол между MN и NP равен углу между BD и AC, который составляет 90 градусов. Следовательно, \(MN \perp NP\).
Четырехугольник MNPQ имеет все стороны равны (\(MN = NP = PQ = QM\)) и один прямой угол (\(\angle MNP = 90^\circ\)). Четырехугольник с равными сторонами является ромбом. Ромб с прямым углом является квадратом.
Следовательно, MNPQ — квадрат.

Ответ: а) \(\vec{DP} = \vec{PC}\); \(\vec{MN} = \vec{QP}\); \(\vec{PN} = \vec{QM}\); б) MNPQ — квадрат.