Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 559 Атанасян — Подробные Ответы
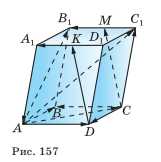
На рисунке 157 изображён параллелепипед \(ABCDA_1B_1C_1D_1\). Точки \(М\) и \(К\) — середины рёбер \(B_1C_1\) и \(A_1D_1\). Укажите на этом рисунке все пары: а) сонаправленных векторов; б) противоположно направленных векторов; в) равных векторов.
Решение: а) Сонаправленные векторы: \(\vec{D_1A_1} \uparrow\uparrow \vec{C_1B_1}\); \(\vec{D_1A_1} \uparrow\uparrow \vec{CB}\); \(\vec{C_1B_1} \uparrow\uparrow \vec{CB}\); \(\vec{DK} \uparrow\uparrow \vec{CM}\) б) Противоположно направленные векторы: \(\vec{A_1A} \uparrow\downarrow \vec{CC_1}\); \(\vec{CD} \uparrow\downarrow \vec{AB}\); \(\vec{D_1A_1} \uparrow\downarrow \vec{AD}\); \(\vec{C_1B_1} \uparrow\downarrow \vec{AD}\); \(\vec{CB} \uparrow\downarrow \vec{AD}\) в) Равные векторы: \(\vec{D_1A_1} = \vec{C_1B_1} = \vec{CB}\); \(\vec{CM} = \vec{DK}\)
Дано: \(ABCDA_1B_1C_1D_1\) — параллелепипед; \(М\) и \(К\) — середины \(B_1C_1\) и \(A_1D_1\). Найти: пары векторов.
Решение:
а) Сонаправленные векторы. Векторы сонаправлены, если они параллельны и направлены в одну сторону. В параллелепипеде противоположные рёбра параллельны и равны по длине. Рассмотрим рёбра \(D_1A_1\), \(C_1B_1\), и \(CB\). Поскольку \(ABCDA_1B_1C_1D_1\) — параллелепипед, грань \(A_1B_1C_1D_1\) является параллелограммом, следовательно, \(D_1A_1 \parallel C_1B_1\). Грань \(A_1AD D_1\) параллельна грани \(B_1BCC_1\), а грань \(ABCD\) параллельна грани \(A_1B_1C_1D_1\). Ребро \(D_1A_1\) параллельно ребру \(AD\), а ребро \(AD\) параллельно ребру \(CB\). Таким образом, \(D_1A_1 \parallel CB\). Аналогично, \(C_1B_1 \parallel AD \parallel CB\). Векторы \(\vec{D_1A_1}\), \(\vec{C_1B_1}\), \(\vec{CB}\) направлены в одну сторону (условно, «вглубь» параллелепипеда по оси, перпендикулярной плоскости \(ABB_1A_1\)). Следовательно, \(\vec{D_1A_1} \uparrow\uparrow \vec{C_1B_1}\), \(\vec{D_1A_1} \uparrow\uparrow \vec{CB}\), \(\vec{C_1B_1} \uparrow\uparrow \vec{CB}\).
Теперь рассмотрим векторы \(\vec{DK}\) и \(\vec{CM}\). Точка \(K\) — середина \(A_1D_1\), точка \(M\) — середина \(B_1C_1\). Поскольку \(A_1D_1 \parallel B_1C_1\) и \(A_1D_1 = B_1C_1\), отрезки \(D_1K\) и \(C_1M\) равны по длине и параллельны. Также рёбра \(DD_1\) и \(CC_1\) параллельны и равны по длине. Рассмотрим треугольники \(\triangle D_1DK\) и \(\triangle C_1CM\). У нас есть \(D_1D = C_1C\) и \(D_1K = C_1M\). Угол между ребром \(DD_1\) и отрезком \(D_1K\) (лежащим на \(D_1A_1\)) равен углу между ребром \(CC_1\) и отрезком \(C_1M\) (лежащим на \(C_1B_1\)), то есть \(\angle DD_1K = \angle CC_1M\), поскольку соответствующие рёбра параллельны (\(DD_1 \parallel CC_1\) и \(D_1A_1 \parallel C_1B_1\)) и плоскости, в которых лежат углы (\(AD_1D\) и \(BC_1C\)), параллельны. Таким образом, треугольники \(\triangle D_1DK\) и \(\triangle C_1CM\) равны по двум сторонам и углу между ними (\(D_1D = C_1C\), \(D_1K = C_1M\), \(\angle DD_1K = \angle CC_1M\)). Из равенства треугольников следует равенство сторон \(DK = CM\). Векторы \(\vec{DK}\) и \(\vec{CM}\) сонаправлены, так как они соединяют соответствующие вершины \(D\) и \(C\) с серединами \(K\) и \(M\) параллельных и равных отрезков \(A_1D_1\) и \(B_1C_1\) соответственно, при этом векторы \(\vec{DD_1}\) и \(\vec{CC_1}\) сонаправлены, и векторы \(\vec{D_1K}\) и \(\vec{C_1M}\) сонаправлены. Следовательно, \(\vec{DK} \uparrow\uparrow \vec{CM}\).
б) Противоположно направленные векторы. Векторы противоположно направлены, если они параллельны и направлены в противоположные стороны. Ребро \(A_1A\) параллельно ребру \(CC_1\), но вектор \(\vec{A_1A}\) направлен от \(A_1\) к \(A\), а вектор \(\vec{CC_1}\) направлен от \(C\) к \(C_1\). Они противоположно направлены: \(\vec{A_1A} \uparrow\downarrow \vec{CC_1}\). Ребро \(CD\) параллельно ребру \(AB\), но вектор \(\vec{CD}\) направлен от \(C\) к \(D\), а вектор \(\vec{AB}\) направлен от \(A\) к \(B\). Они противоположно направлены: \(\vec{CD} \uparrow\downarrow \vec{AB}\). Ребро \(D_1A_1\) параллельно ребру \(AD\), но вектор \(\vec{D_1A_1}\) направлен от \(D_1\) к \(A_1\), а вектор \(\vec{AD}\) направлен от \(A\) к \(D\). Они противоположно направлены: \(\vec{D_1A_1} \uparrow\downarrow \vec{AD}\). Ребро \(C_1B_1\) параллельно ребру \(AD\), но вектор \(\vec{C_1B_1}\) направлен от \(C_1\) к \(B_1\), а вектор \(\vec{AD}\) направлен от \(A\) к \(D\). Они противоположно направлены: \(\vec{C_1B_1} \uparrow\downarrow \vec{AD}\). Ребро \(CB\) параллельно ребру \(AD\), но вектор \(\vec{CB}\) направлен от \(C\) к \(B\), а вектор \(\vec{AD}\) направлен от \(A\) к \(D\). Они противоположно направлены: \(\vec{CB} \uparrow\downarrow \vec{AD}\).
в) Равные векторы. Равные векторы сонаправлены и имеют равные длины. Из пункта а) мы знаем, что векторы \(\vec{D_1A_1}\), \(\vec{C_1B_1}\), и \(\vec{CB}\) сонаправлены. Длины этих векторов равны как длины противоположных рёбер параллелограммов \(A_1B_1C_1D_1\) и \(ABCD\), и поскольку \(A_1B_1C_1D_1\) конгруэнтен \(ABCD\). Следовательно, \(\vec{D_1A_1} = \vec{C_1B_1} = \vec{CB}\). Из пункта а) мы также установили, что векторы \(\vec{CM}\) и \(\vec{DK}\) сонаправлены и из равенства треугольников \(\triangle D_1DK\) и \(\triangle C_1CM\) следует равенство их длин \(CM = DK\). Таким образом, векторы \(\vec{CM}\) и \(\vec{DK}\) равны: \(\vec{CM} = \vec{DK}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.