
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 558 Атанасян — Подробные Ответы
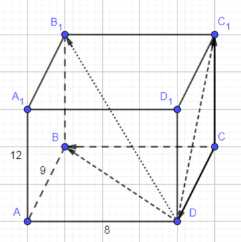
Измерения прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\) имеют следующие значения: \(AD = 8\) см, \(АВ = 9\) см и \(АА_1 = 12\) см. Найдите длины векторов: а) \(\vec{CC_1}\), \(\vec{CB}\), \(\vec{CD}\); б) \(\vec{DC_1}\), \(\vec{DB}\), \(\vec{DB_1}\).
а) Длины векторов равны: \(|\vec{CC_1}| = CC_1 = AA_1 = 12\) см, \(|\vec{CB}| = CB = AD = 8\) см, \(|\vec{CD}| = CD = AB = 9\) см. б) Длины векторов равны: \(|\vec{DC_1}| = \sqrt{DC^2 + CC_1^2} = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15\) см, \(|\vec{DB}| = \sqrt{AB^2 + AD^2} = \sqrt{9^2 + 8^2} = \sqrt{81 + 64} = \sqrt{145}\) см, \(|\vec{DB_1}| = \sqrt{DB^2 + BB_1^2} = \sqrt{(\sqrt{145})^2 + 12^2} = \sqrt{145 + 144} = \sqrt{289} = 17\) см.
Дан прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\) с измерениями \(AD = 8\) см, \(АВ = 9\) см и \(АА_1 = 12\) см. Требуется найти длины векторов: а) \(\vec{CC_1}\), \(\vec{CB}\), \(\vec{CD}\) и б) \(\vec{DC_1}\), \(\vec{DB}\), \(\vec{DB_1}\).
а) Найдем длины векторов \(\vec{CC_1}\), \(\vec{CB}\), \(\vec{CD}\).
В прямоугольном параллелепипеде противоположные ребра равны и параллельны.
Вектор \(\vec{CC_1}\) направлен вдоль ребра \(CC_1\). Длина этого вектора равна длине ребра \(CC_1\). Поскольку \(ABCDA_1B_1C_1D_1\) — параллелепипед, ребра \(CC_1\), \(BB_1\), \(AA_1\), \(DD_1\) параллельны и равны по длине. Дано, что \(AA_1 = 12\) см. Следовательно, длина вектора \(\vec{CC_1}\) равна \(||\vec{CC_1}|| = CC_1 = AA_1 = 12\) см.
Вектор \(\vec{CB}\) направлен вдоль ребра \(CB\). Длина этого вектора равна длине ребра \(CB\). В параллелепипеде \(ABCDA_1B_1C_1D_1\) ребра \(CB\) и \(AD\) параллельны и равны по длине. Дано, что \(AD = 8\) см. Следовательно, длина вектора \(\vec{CB}\) равна \(||\vec{CB}|| = CB = AD = 8\) см.
Вектор \(\vec{CD}\) направлен вдоль ребра \(CD\). Длина этого вектора равна длине ребра \(CD\). В параллелепипеде \(ABCDA_1B_1C_1D_1\) ребра \(CD\) и \(AB\) параллельны и равны по длине. Дано, что \(AB = 9\) см. Следовательно, длина вектора \(\vec{CD}\) равна \(||\vec{CD}|| = CD = AB = 9\) см.
б) Найдем длины векторов \(\vec{DC_1}\), \(\vec{DB}\), \(\vec{DB_1}\).
Вектор \(\vec{DC_1}\) является диагональю грани \(DCC_1D_1\). Грани прямоугольного параллелепипеда являются прямоугольниками. Рассмотрим прямоугольник \(DCC_1D_1\). В нем ребра \(DC\) и \(CC_1\) перпендикулярны. Длина ребра \(DC\) равна \(AB = 9\) см, а длина ребра \(CC_1\) равна \(AA_1 = 12\) см. По теореме Пифагора в прямоугольном треугольнике \(DCC_1\) с прямым углом при вершине \(C\), длина диагонали \(DC_1\) равна корню квадратному из суммы квадратов длин катетов \(DC\) и \(CC_1\). Следовательно, длина вектора \(\vec{DC_1}\) равна \(||\vec{DC_1}|| = DC_1 = \sqrt{DC^2 + CC_1^2} = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15\) см.
Вектор \(\vec{DB}\) является диагональю грани \(ABCD\). Грани прямоугольного параллелепипеда являются прямоугольниками. Рассмотрим прямоугольник \(ABCD\). В нем ребра \(AB\) и \(AD\) перпендикулярны. Длина ребра \(AB\) равна 9 см, а длина ребра \(AD\) равна 8 см. По теореме Пифагора в прямоугольном треугольнике \(ABD\) с прямым углом при вершине \(A\), длина диагонали \(DB\) равна корню квадратному из суммы квадратов длин катетов \(AB\) и \(AD\). Следовательно, длина вектора \(\vec{DB}\) равна \(||\vec{DB}|| = DB = \sqrt{AB^2 + AD^2} = \sqrt{9^2 + 8^2} = \sqrt{81 + 64} = \sqrt{145}\) см.
Вектор \(\vec{DB_1}\) является пространственной диагональю параллелепипеда. Рассмотрим прямоугольный треугольник \(DBB_1\). В нем ребро \(BB_1\) перпендикулярно плоскости основания \(ABCD\), а значит, перпендикулярно любой прямой в этой плоскости, проходящей через точку \(B\), включая диагональ \(DB\). Таким образом, треугольник \(DBB_1\) является прямоугольным с прямым углом при вершине \(B\). Длина катета \(BB_1\) равна \(AA_1 = 12\) см. Длина катета \(DB\) была найдена ранее и равна \(\sqrt{145}\) см. По теореме Пифагора в прямоугольном треугольнике \(DBB_1\), длина диагонали \(DB_1\) равна корню квадратному из суммы квадратов длин катетов \(DB\) и \(BB_1\). Следовательно, длина вектора \(\vec{DB_1}\) равна \(||\vec{DB_1}|| = DB_1 = \sqrt{DB^2 + BB_1^2} = \sqrt{(\sqrt{145})^2 + 12^2} = \sqrt{145 + 144} =\)
\(= \sqrt{289} = 17\) см.
Таким образом, длины векторов равны: а) 12 см, 8 см, 9 см; б) 15 см, \(\sqrt{145}\) см, 17 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!