ГДЗ по Геометрии 11 класс Номер 557 Атанасян — Подробные Ответы

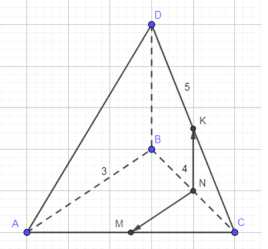
В тетраэдре \(ABCD\) точки \(M\), \(N\) и \(К\) — середины рёбер \(AC\), \(ВС\) и \(CD\) соответственно, \(АВ = 3\) см, \(ВС = 4\) см, \(BD = 5\) см. Найдите длины векторов: а) \(\vec{AB}\), \(\vec{BC}\), \(\vec{BD}\), \(\vec{NM}\), \(\vec{BN}\), \(\vec{NK}\); б) \(\vec{CB}\), \(\vec{BA}\), \(\vec{DB}\), \(\vec{NC}\), \(\vec{KN}\).

В тетраэдре \(ABCD\) дано, что \(M\), \(N\), \(K\) — середины рёбер \(AC\), \(BC\), \(CD\) соответственно. Известны длины рёбер: \(AB = 3\) см, \(BC = 4\) см, \(BD = 5\) см. Требуется найти длины векторов.

Решение:
а) Длины векторов \(\vec{AB}\), \(\vec{BC}\), \(\vec{BD}\), \(\vec{NM}\), \(\vec{BN}\), \(\vec{NK}\).
Длины векторов, совпадающих с рёбрами, равны длинам рёбер: \(|\vec{AB}| = AB = 3\) см, \(|\vec{BC}| = BC = 4\) см, \(|\vec{BD}| = BD = 5\) см.
Так как \(N\) — середина \(BC\) и \(M\) — середина \(AC\), отрезок \(NM\) является средней линией треугольника \(ABC\). Длина средней линии равна половине длины стороны, которой она параллельна. Следовательно, \(|\vec{NM}| = NM = \frac{1}{2}AB = \frac{1}{2} \cdot 3 = 1.5\) см.
Так как \(N\) — середина \(BC\), длина вектора \(\vec{BN}\) равна половине длины ребра \(BC\): \(|\vec{BN}| = BN = \frac{1}{2}BC = \frac{1}{2} \cdot 4 = 2\) см.
Так как \(N\) — середина \(BC\) и \(K\) — середина \(CD\), отрезок \(NK\) является средней линией треугольника \(BCD\). Длина средней линии равна половине длины стороны, которой она параллельна. Следовательно, \(|\vec{NK}| = NK = \frac{1}{2}BD = \frac{1}{2} \cdot 5 = 2.5\) см.

б) Длины векторов \(\vec{CB}\), \(\vec{BA}\), \(\vec{DB}\), \(\vec{NC}\), \(\vec{KN}\).
Длины векторов, противоположных векторам рёбер, равны длинам соответствующих рёбер: \(|\vec{CB}| = CB = BC = 4\) см, \(|\vec{BA}| = BA = AB = 3\) см, \(|\vec{DB}| = DB = BD = 5\) см.
Так как \(N\) — середина \(BC\), длина вектора \(\vec{NC}\) равна половине длины ребра \(BC\): \(|\vec{NC}| = NC = \frac{1}{2}BC = \frac{1}{2} \cdot 4 = 2\) см.
Так как \(K\) — середина \(CD\) и \(N\) — середина \(BC\), отрезок \(KN\) является средней линией треугольника \(BCD\). Длина средней линии равна половине длины стороны, которой она параллельна. Следовательно, \(|\vec{KN}| = KN = \frac{1}{2}BD = \frac{1}{2} \cdot 5 = 2.5\) см.

Ответ: а) 3 см, 4 см, 5 см, 1.5 см, 2 см, 2.5 см; б) 4 см, 3 см, 5 см, 2 см, 2.5 см.

В данном тетраэдре \(ABCD\) заданы положения точек \(M\), \(N\) и \(K\) как середины рёбер \(AC\), \(BC\) и \(CD\) соответственно. Также известны длины некоторых рёбер тетраэдра: \(AB = 3\) см, \(BC = 4\) см, \(BD = 5\) см. Требуется определить длины заданных векторов.

Решение задачи состоит из двух частей, соответствующих пунктам а) и б).

а) Находим длины векторов \(\vec{AB}\), \(\vec{BC}\), \(\vec{BD}\), \(\vec{NM}\), \(\vec{BN}\), \(\vec{NK}\).
Длина вектора \(\vec{AB}\) равна длине ребра \(AB\), так как вектор совпадает с ребром по направлению и величине. Следовательно, \(|\vec{AB}| = AB = 3\) см.
Аналогично, длина вектора \(\vec{BC}\) равна длине ребра \(BC\): \(|\vec{BC}| = BC = 4\) см.
Длина вектора \(\vec{BD}\) равна длине ребра \(BD\): \(|\vec{BD}| = BD = 5\) см.
Вектор \(\vec{NM}\) соединяет середину ребра \(BC\) (точка \(N\)) и середину ребра \(AC\) (точка \(M\)). Отрезок \(NM\) является средней линией треугольника \(ABC\). По свойству средней линии треугольника, её длина равна половине длины стороны, которой она параллельна. Отрезок \(NM\) параллелен ребру \(AB\), поэтому его длина \(NM = \frac{1}{2}AB\). Подставляя известное значение \(AB = 3\) см, получаем \(|\vec{NM}| = NM = \frac{1}{2} \cdot 3 = 1.5\) см.
Вектор \(\vec{BN}\) направлен из вершины \(B\) в середину ребра \(BC\) (точка \(N\)). Его длина равна половине длины ребра \(BC\). Подставляя известное значение \(BC = 4\) см, получаем \(|\vec{BN}| = BN = \frac{1}{2}BC = \frac{1}{2} \cdot 4 = 2\) см.
Вектор \(\vec{NK}\) соединяет середину ребра \(BC\) (точка \(N\)) и середину ребра \(CD\) (точка \(K\)). Отрезок \(NK\) является средней линией треугольника \(BCD\). По свойству средней линии треугольника, её длина равна половине длины стороны, которой она параллельна. Отрезок \(NK\) параллелен ребру \(BD\), поэтому его длина \(NK = \frac{1}{2}BD\). Подставляя известное значение \(BD = 5\) см, получаем \(|\vec{NK}| = NK = \frac{1}{2} \cdot 5 = 2.5\) см.

б) Находим длины векторов \(\vec{CB}\), \(\vec{BA}\), \(\vec{DB}\), \(\vec{NC}\), \(\vec{KN}\).
Вектор \(\vec{CB}\) является противоположным вектору \(\vec{BC}\). Длина противоположного вектора равна длине исходного вектора. Следовательно, \(|\vec{CB}| = |\vec{BC}| = 4\) см.
Вектор \(\vec{BA}\) является противоположным вектору \(\vec{AB}\). Его длина равна длине вектора \(\vec{AB}\). Следовательно, \(|\vec{BA}| = |\vec{AB}| = 3\) см.
Вектор \(\vec{DB}\) является противоположным вектору \(\vec{BD}\). Его длина равна длине вектора \(\vec{BD}\). Следовательно, \(|\vec{DB}| = |\vec{BD}| = 5\) см.
Вектор \(\vec{NC}\) направлен из середины ребра \(BC\) (точка \(N\)) в вершину \(C\). Его длина равна половине длины ребра \(BC\). Подставляя известное значение \(BC = 4\) см, получаем \(|\vec{NC}| = NC = \frac{1}{2}BC = \frac{1}{2} \cdot 4 = 2\) см.
Вектор \(\vec{KN}\) соединяет середину ребра \(CD\) (точка \(K\)) и середину ребра \(BC\) (точка \(N\)). Отрезок \(KN\) является средней линией треугольника \(BCD\). По свойству средней линии треугольника, её длина равна половине длины стороны, которой она параллельна. Отрезок \(KN\) параллелен ребру \(BD\), поэтому его длина \(KN = \frac{1}{2}BD\). Подставляя известное значение \(BD = 5\) см, получаем \(|\vec{KN}| = KN = \frac{1}{2} \cdot 5 = 2.5\) см. Обратите внимание, что \(|\vec{KN}| = |\vec{NK}|\).

Таким образом, получены следующие длины векторов.
а) 3 см, 4 см, 5 см, 1.5 см, 2 см, 2.5 см.
б) 4 см, 3 см, 5 см, 2 см, 2.5 см.