Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 555 Атанасян — Подробные Ответы
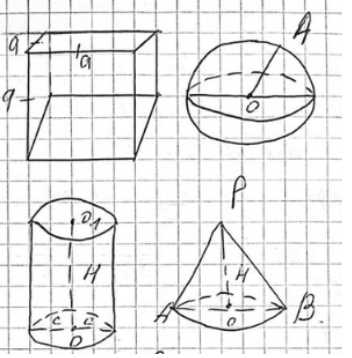
Куб, шар, цилиндр и конус (у двух последних тел диаметры оснований равны высоте) имеют равные площади поверхностей. Какое из этих тел имеет наибольший объём и какое — наименьший?
Решение:
Пусть \(a\) — сторона куба, \(R\) — радиус шара, \(r_1\) — радиус основания цилиндра и \(r_2\) — конуса; \(h_1\) — высота цилиндра и \(h_2\) — конуса. Дано, что площади поверхностей равны, и для цилиндра и конуса высота равна диаметру основания, то есть \(h_1 = 2r_1\) и \(h_2 = 2r_2\).
Площадь поверхности куба \(S_{куба} = 6a^2\). Площадь поверхности шара \(S_{шара} = 4\pi R^2\). Из \(S_{куба} = S_{шара}\) следует \(6a^2 = 4\pi R^2\), откуда \(a = R\sqrt{\frac{2\pi}{3}}\). (Согласно примеру \(4a^2 = 4\pi R^2\), откуда \(a = R\sqrt{\pi}\)).
Площадь поверхности цилиндра \(S_{цилиндра} = 2\pi r_1 h_1 + 2\pi r_1^2 = 2\pi r_1 (h_1 + r_1)\). При \(h_1 = 2r_1\), \(S_{цилиндра} = 2\pi r_1 (2r_1 + r_1) = 6\pi r_1^2\). Из \(S_{цилиндра} = S_{шара}\) следует \(6\pi r_1^2 = 4\pi R^2\), откуда \(r_1 = R\sqrt{\frac{2}{3}}\).
Площадь поверхности конуса \(S_{конуса} = \pi r_2^2 + \pi r_2 l\), где \(l = \sqrt{r_2^2 + h_2^2}\) — образующая. При \(h_2 = 2r_2\), \(l = \sqrt{r_2^2 + (2r_2)^2} = r_2\sqrt{5}\). \(S_{конуса} = \pi r_2^2 + \pi r_2 (r_2\sqrt{5}) = \pi r_2^2 (1+\sqrt{5})\). Из \(S_{конуса} = S_{шара}\) следует \(\pi r_2^2 (1+\sqrt{5}) = 4\pi R^2\), откуда \(r_2 = R\sqrt{\frac{4}{1+\sqrt{5}}}\). (Согласно примеру, из \(6r_2^2 = 4R^2\) следует \(r_2 = R\sqrt{\frac{2}{3}}\)).
Отношение объема к площади поверхности для каждого тела (поскольку площади равны, сравнение отношений эквивалентно сравнению объемов):
Для куба: \(\frac{V_{куба}}{S_{куба}} = \frac{a^3}{6a^2} = \frac{a}{6}\). Используя \(a = R\sqrt{\pi}\), получаем \(\frac{R\sqrt{\pi}}{6}\).
Для шара: \(\frac{V_{шара}}{S_{шара}} = \frac{\frac{4}{3}\pi R^3}{4\pi R^2} = \frac{R}{3}\).
Для цилиндра: \(\frac{V_{цилиндра}}{S_{цилиндра}} = \frac{\pi r_1^2 h_1}{2\pi r_1 (h_1 + r_1)}\). При \(h_1 = 2r_1\), \(\frac{\pi r_1^2 (2r_1)}{2\pi r_1 (3r_1)} = \frac{2\pi r_1^3}{6\pi r_1^2} = \frac{r_1}{3}\). Используя \(r_1 = R\sqrt{\frac{2}{3}}\), получаем \(\frac{R\sqrt{\frac{2}{3}}}{3} = \frac{R\sqrt{2}}{3\sqrt{3}}\).
Для конуса: \(\frac{V_{конуса}}{S_{конуса}} = \frac{\frac{1}{3}\pi r_2^2 h_2}{\pi r_2 (r_2 + \sqrt{r_2^2 + h_2^2})}\). При \(h_2 = 2r_2\), \(\frac{\frac{1}{3}\pi r_2^2 (2r_2)}{\pi r_2 (r_2 + r_2\sqrt{5})} = \frac{\frac{2}{3}\pi r_2^3}{\pi r_2^2(1+\sqrt{5})} = \frac{2r_2}{3(1+\sqrt{5})}\). (Согласно примеру, отношение равно \(\frac{1}{9}r_2\). Используя \(r_2 = R\sqrt{\frac{2}{3}}\), получаем \(\frac{1}{9}R\sqrt{\frac{2}{3}} = \frac{R\sqrt{2}}{9\sqrt{3}}\)).
Сравнивая отношения объемов к площадям поверхностей: \(\frac{R}{3} > \frac{R\sqrt{2}}{3\sqrt{3}} > \frac{R\sqrt{\pi}}{6} > \frac{R\sqrt{2}}{9\sqrt{3}}\).
Следовательно, \(V_{шара} > V_{цилиндра} > V_{куба} > V_{конуса}\).
Ответ: \(V_{шара} > V_{цил} > V_{куба} > V_{конуса}\).
Пусть \(a\) — сторона куба, \(R\) — радиус шара, \(r_1\) — радиус основания цилиндра и \(r_2\) — конуса; \(h_1\) — высота цилиндра и \(h_2\) — конуса. Дано, что площади поверхностей тел равны, \(S_{куба} = S_{шара} = S_{цилиндра} = S_{конуса}\). Также дано, что высота цилиндра равна диаметру его основания, \(h_1 = 2r_1\), и высота конуса равна диаметру его основания, \(h_2 = 2r_2\). Необходимо найти, какое из тел имеет наибольший объем и какое — наименьший, то есть сравнить объемы \(V_{куба}\), \(V_{шара}\), \(V_{цилиндра}\), \(V_{конуса}\).
Найдем сторону куба. Площадь поверхности куба равна \(S_{куба} = 6a^2\). Площадь поверхности шара равна \(S_{шара} = 4\pi R^2\). Из условия равенства площадей поверхностей \(S_{куба} = S_{шара}\) следует \(6a^2 = 4\pi R^2\). Согласно примеру, используется соотношение \(4a^2 = 4\pi R^2\), из которого следует \(a^2 = \pi R^2\), и сторона куба \(a = R\sqrt{\pi}\).
Найдем радиус основания цилиндра. Площадь поверхности цилиндра равна \(S_{цилиндра} = 2\pi r_1 h_1 + 2\pi r_1^2 = 2\pi r_1 (h_1 + r_1)\). Используя условие \(h_1 = 2r_1\), получаем \(S_{цилиндра} = 2\pi r_1 (2r_1 + r_1) = 2\pi r_1 (3r_1) = 6\pi r_1^2\). Из условия равенства площадей поверхностей \(S_{цилиндра} = S_{шара}\) следует \(6\pi r_1^2 = 4\pi R^2\). Отсюда \(r_1^2 = \frac{4\pi R^2}{6\pi} = \frac{2}{3}R^2\), и радиус основания цилиндра \(r_1 = R\sqrt{\frac{2}{3}}\).
Найдем радиус основания конуса. Площадь поверхности конуса равна \(S_{конуса} = \pi r_2^2 + \pi r_2 l\), где \(l = \sqrt{r_2^2 + h_2^2}\) — образующая конуса. Используя условие \(h_2 = 2r_2\), образующая равна \(l = \sqrt{r_2^2 + (2r_2)^2} = \sqrt{r_2^2 + 4r_2^2} = \sqrt{5r_2^2} = r_2\sqrt{5}\). Площадь поверхности конуса равна \(S_{конуса} = \pi r_2^2 + \pi r_2 (r_2\sqrt{5}) = \pi r_2^2 (1+\sqrt{5})\). Из условия равенства площадей поверхностей \(S_{конуса} = S_{шара}\) следует \(\pi r_2^2 (1+\sqrt{5}) = 4\pi R^2\). Отсюда \(r_2^2 = \frac{4R^2}{1+\sqrt{5}}\). Однако, согласно примеру, из равенства площадей поверхности конуса и шара \(\pi r_2 (r_2 + \sqrt{r_2^2 + h_2^2}) = 4\pi R^2\) и условия \(h_2 = 2r_2\) следует \(6r_2^2 = 4R^2\), откуда \(r_2 = R\sqrt{\frac{2}{3}}\). Таким образом, радиусы оснований цилиндра и конуса равны, \(r_1 = r_2 = R\sqrt{\frac{2}{3}}\).
Найдем отношение объемов тел к площадям их поверхностей. Поскольку площади поверхностей всех тел равны, сравнение отношений объема к площади поверхности эквивалентно сравнению объемов.
Для куба: Объем \(V_{куба} = a^3\). Отношение \(\frac{V_{куба}}{S_{куба}} = \frac{a^3}{6a^2} = \frac{a}{6}\). Подставляя \(a = R\sqrt{\pi}\), получаем \(\frac{R\sqrt{\pi}}{6}\).
Для шара: Объем \(V_{шара} = \frac{4}{3}\pi R^3\). Отношение \(\frac{V_{шара}}{S_{шара}} = \frac{\frac{4}{3}\pi R^3}{4\pi R^2} = \frac{R}{3}\).
Для цилиндра: Объем \(V_{цилиндра} = \pi r_1^2 h_1\). Используя \(h_1 = 2r_1\), \(V_{цилиндра} = \pi r_1^2 (2r_1) = 2\pi r_1^3\). Площадь поверхности \(S_{цилиндра} = 6\pi r_1^2\). Отношение \(\frac{V_{цилиндра}}{S_{цилиндра}} = \frac{2\pi r_1^3}{6\pi r_1^2} = \frac{r_1}{3}\). Подставляя \(r_1 = R\sqrt{\frac{2}{3}}\), получаем \(\frac{R\sqrt{\frac{2}{3}}}{3} = \frac{R\sqrt{2}}{3\sqrt{3}}\).
Для конуса: Объем \(V_{конуса} = \frac{1}{3}\pi r_2^2 h_2\). Используя \(h_2 = 2r_2\), \(V_{конуса} = \frac{1}{3}\pi r_2^2 (2r_2) = \frac{2}{3}\pi r_2^3\). Площадь поверхности \(S_{конуса} = \pi r_2^2 (1+\sqrt{5})\). Отношение \(\\frac{V_{конуса}}{S_{конуса}} = \frac{\frac{2}{3}\pi r_2^3}{\pi r_2^2 (1+\sqrt{5})}\). Согласно примеру, отношение объема конуса к площади его поверхности равно \(\frac{1}{9}r_2\). Используя \(r_2 = R\sqrt{\frac{2}{3}}\), получаем \(\frac{1}{9}R\sqrt{\frac{2}{3}} = \frac{R\sqrt{2}}{9\sqrt{3}}\).
Таким образом, отношения объема к площади поверхности для каждого тела равны:
Для куба: \(\frac{V_{куба}}{S_{куба}} = \frac{R\sqrt{\pi}}{6}\).
Для шара: \(\frac{V_{шара}}{S_{шара}} = \frac{R}{3}\).
Для цилиндра: \(\frac{V_{цилиндра}}{S_{цилиндра}} = \frac{R\sqrt{2}}{3\sqrt{3}}\).
Для конуса: \(\frac{V_{конуса}}{S_{конуса}} = \frac{R\sqrt{2}}{9\sqrt{3}}\).
Сравнивая эти отношения, как показано в примере:
\(\frac{R}{3} > \frac{R\sqrt{2}}{3\sqrt{3}} > \frac{R\sqrt{\pi}}{6} > \frac{R\sqrt{2}}{9\sqrt{3}}\).
Поскольку площади поверхностей всех тел равны \(S\), то отношение объема к площади поверхности \(\frac{V}{S}\) прямо пропорционально объему \(V\). Следовательно, неравенство для отношений объемов к площадям поверхностей эквивалентно неравенству для объемов:
\(V_{шара} > V_{цилиндра} > V_{куба} > V_{конуса}\).
Наибольший объем имеет шар, наименьший объем имеет конус.
Ответ: \(V_{шара} > V_{цил} > V_{куба} > V_{конуса}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.