
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 553 Атанасян — Подробные Ответы
В шар вписана пирамида, основанием которой является прямоугольник с диагональю 10 см. Каждое боковое ребро пирамиды составляет с основанием угол \(\beta\). Найдите площадь поверхности и объём шара.
Общий объем двух шаровых сегментов \(V_{\text{ш}} = 2\pi h^2 (r — \frac{h}{3})\). При \(r = 1.5\) и \(h = 0.5\), \(V_{\text{ш}} = 2\pi (0.5)^2 (1.5 — \frac{0.5}{3}) = 0.5\pi (1.5 — \frac{1}{6}) = 0.5\pi (\frac{9-1}{6}) = 0.5\pi \frac{8}{6} = \frac{2}{3}\pi\). Объем цилиндра \(V_{\text{цил}} = \pi r^2 l = \pi (1.5)^2 l = 2.25\pi l\). Общий объем \(V = V_{\text{ш}} + V_{\text{цил}}\), то есть \(50 = \frac{2}{3}\pi + 2.25\pi l\). Выражая \(l\), получаем \(l = \frac{50 — \frac{2}{3}\pi}{2.25\pi}\). Используя \(\pi \approx 3.14\), \(l \approx \frac{50 — \frac{2}{3} \cdot 3.14}{2.25 \cdot 3.14} \approx \frac{50 — 2.0933}{7.065} \approx \frac{47.9067}{7.065} \approx 6.8\).
Ответ \(l = 6.8\) м.
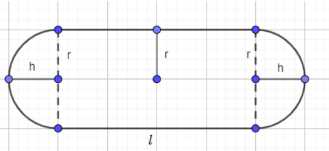
Данная задача описывает составное тело, состоящее из центрального цилиндра и двух одинаковых шаровых сегментов, расположенных по его торцам. Общий объем этого тела равен сумме объемов двух шаровых сегментов и объема цилиндра.
Сначала найдем объем двух шаровых сегментов. Объем одного шарового сегмента радиусом сферы \(r\) и высотой \(h\) определяется формулой \(V_{\text{сегмента}} = \frac{1}{3}\pi h^2 (3r — h)\). В данном случае радиус сферы \(r = 1.5\) м и высота каждого сегмента \(h = 0.5\) м. Объем двух таких сегментов будет \(V_{\text{ш}} = 2 \times V_{\text{сегмента}} = 2 \times \frac{1}{3}\pi h^2 (3r — h)\). Подставим известные значения: \(V_{\text{ш}} = \frac{2}{3}\pi (0.5)^2 (3 \times 1.5 — 0.5)\). Вычислим значение в скобках: \(3 \times 1.5 — 0.5 = 4.5 — 0.5 = 4\). Значение \(h^2 = (0.5)^2 = 0.25\). Теперь подставим эти значения обратно в формулу для \(V_{\text{ш}}\): \(V_{\text{ш}} = \frac{2}{3}\pi (0.25) (4)\). Умножим числа: \(0.25 \times 4 = 1\). Следовательно, объем двух шаровых сегментов равен \(V_{\text{ш}} = \frac{2}{3}\pi \times 1 = \frac{2}{3}\pi\) кубических метров.
Далее найдем объем цилиндра. Объем цилиндра радиусом основания \(r\) и высотой (длиной образующей) \(l\) определяется формулой \(V_{\text{цилиндра}} = \pi r^2 l\). Радиус основания цилиндра равен радиусу сферы, то есть \(r = 1.5\) м. Подставим это значение в формулу: \(V_{\text{цилиндра}} = \pi (1.5)^2 l\). Вычислим \(1.5^2 = 2.25\). Таким образом, объем цилиндра равен \(V_{\text{цилиндра}} = 2.25\pi l\) кубических метров.
Общий объем составного тела равен сумме объемов двух шаровых сегментов и объема цилиндра: \(V = V_{\text{ш}} + V_{\text{цилиндра}}\). По условию задачи общий объем \(V = 50\) кубических метров. Подставим найденные выражения для объемов сегментов и цилиндра в это уравнение: \(50 = \frac{2}{3}\pi + 2.25\pi l\).
Теперь необходимо решить это уравнение относительно неизвестной длины образующей цилиндра \(l\). Перенесем член с \(\pi\) без \(l\) в левую часть уравнения: \(50 — \frac{2}{3}\pi = 2.25\pi l\). Чтобы найти \(l\), разделим обе части уравнения на \(2.25\pi\): \(l = \frac{50 — \frac{2}{3}\pi}{2.25\pi}\).
Теперь подставим приближенное значение \(\pi \approx 3.14\) для получения численного результата. Сначала вычислим \(\frac{2}{3}\pi \approx \frac{2}{3} \times 3.14 \approx 2.0933\). Затем вычислим \(2.25\pi \approx 2.25 \times 3.14 \approx 7.065\). Теперь подставим эти значения в формулу для \(l\): \(l \approx \frac{50 — 2.0933}{7.065}\). Вычислим разность в числителе: \(50 — 2.0933 = 47.9067\). Теперь выполним деление: \(l \approx \frac{47.9067}{7.065} \approx 6.7806\).
Результат необходимо округлить до одного знака после запятой. Смотрим на вторую цифру после запятой, это 8. Поскольку 8 больше или равно 5, округляем первую цифру после запятой (7) в большую сторону. Получаем \(l \approx 6.8\).
Таким образом, длина образующей цилиндра составляет приблизительно 6.8 метра.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!