Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 551 Атанасян — Подробные Ответы
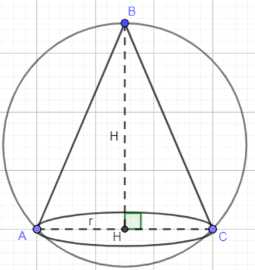
В шар вписан конус, радиус основания которого равен \(r\), а высота равна \(Н\). Найдите площадь поверхности и объём шара.
Высота конуса равна \(H\), радиус основания конуса равен \(r\). Радиус шара, описанного около конуса, находится по формуле \(R_{\text{шара}} = \frac{l^2}{2H}\), где \(l\) — образующая конуса. Образующая конуса \(l\) может быть найдена по теореме Пифагора: \(l^2 = H^2 + r^2\). Следовательно, радиус шара равен \(R_{\text{шара}} = \frac{H^2 + r^2}{2H}\). Площадь поверхности шара находится по формуле \(S_{\text{шара}} = 4\pi R_{\text{шара}}^2\). Подставляя значение \(R_{\text{шара}}\), получаем \(S_{\text{шара}} = 4\pi \left(\frac{H^2 + r^2}{2H}\right)^2 = 4\pi \frac{(H^2 + r^2)^2}{4H^2} = \frac{\pi (H^2 + r^2)^2}{H^2}\). Объём шара находится по формуле \(V_{\text{шара}} = \frac{4}{3}\pi R_{\text{шара}}^3\). Подставляя значение \(R_{\text{шара}}\), получаем \(V_{\text{шара}} = \frac{4}{3}\pi \left(\frac{H^2 + r^2}{2H}\right)^3 = \frac{4}{3}\pi \frac{(H^2 + r^2)^3}{8H^3} = \frac{\pi (H^2 + r^2)^3}{6H^3}\). Ответ: \(S_{\text{шара}} = \frac{\pi (H^2 + r^2)^2}{H^2}\), \(V_{\text{шара}} = \frac{\pi (H^2 + r^2)^3}{6H^3}\).
Пусть дан шар с центром в точке \(O\), в который вписан конус с радиусом основания \(r\) и высотой \(H\). Требуется найти площадь поверхности шара \(S_{\text{шара}}\) и объём шара \(V_{\text{шара}}\).
Обозначим высоту конуса как \(CH\), где \(C\) — вершина конуса, а \(H\) — центр основания. Тогда по условию \(CH = H\). Радиус основания конуса — это отрезок \(AH\) (или \(BH\)), где \(A\) и \(B\) — точки на окружности основания. По условию \(AH = r\). Радиус шара обозначим \(R_{\text{шара}}\). Поскольку шар описан около конуса, вершина конуса \(C\) и все точки окружности основания лежат на поверхности шара. Центр шара \(O\) лежит на оси конуса \(CH\). Расстояние от центра шара до любой точки на его поверхности равно радиусу шара, то есть \(OA = OB = OC = R_{\text{шара}}\).
Рассмотрим осевое сечение конуса, которое представляет собой равнобедренный треугольник \(ABC\). Основание этого треугольника \(AB\) является диаметром основания конуса, поэтому \(AB = 2 \cdot AH = 2r\). Боковые стороны \(AC\) и \(BC\) являются образующими конуса. Поскольку треугольник \(ABC\) является осевым сечением конуса, вписанного в шар, окружность, описанная около треугольника \(ABC\), является большим кругом шара, и радиус этой окружности равен радиусу шара \(R_{\text{шара}}\).
Найдем длину образующей \(AC\). Рассмотрим прямоугольный треугольник \(ACH\), где \(CH\) — высота конуса и \(AH\) — радиус основания. По теореме Пифагора, квадрат образующей равен сумме квадратов высоты и радиуса основания: \(AC^2 = CH^2 + AH^2\). Подставляя известные значения, получаем \(AC^2 = H^2 + r^2\). Следовательно, длина образующей \(AC = \sqrt{H^2 + r^2}\). Поскольку треугольник \(ABC\) равнобедренный с основанием \(AB\), \(BC = AC = \sqrt{H^2 + r^2}\).
Теперь найдем радиус шара \(R_{\text{шара}}\), который является радиусом окружности, описанной около треугольника \(ABC\). Радиус описанной окружности для любого треугольника можно найти по формуле \(R = \frac{abc}{4S}\), где \(a, b, c\) — длины сторон треугольника, а \(S\) — его площадь. В нашем случае стороны треугольника \(ABC\) имеют длины \(a = AB = 2r\), \(b = AC = \sqrt{H^2 + r^2}\), и \(c = BC = \sqrt{H^2 + r^2}\). Площадь треугольника \(ABC\) можно найти как половину произведения основания на высоту: \(S_{ABC} = \frac{1}{2} \cdot AB \cdot CH\). Подставляя значения \(AB = 2r\) и \(CH = H\), получаем \(S_{ABC} = \frac{1}{2} \cdot (2r) \cdot H = rH\).
Теперь подставим длины сторон и площадь в формулу для радиуса описанной окружности: \(R_{\text{шара}} = \frac{AB \cdot AC \cdot BC}{4S_{ABC}} = \frac{(2r) \cdot (\sqrt{H^2 + r^2}) \cdot (\sqrt{H^2 + r^2})}{4(rH)}\). Упростим это выражение: \(R_{\text{шара}} = \frac{2r (H^2 + r^2)}{4rH}\). Сокращая \(2r\) в числителе и знаменателе, получаем \(R_{\text{шара}} = \frac{H^2 + r^2}{2H}\).
Теперь, зная радиус шара \(R_{\text{шара}}\), можем найти площадь его поверхности. Площадь поверхности шара находится по формуле \(S_{\text{шара}} = 4\pi R_{\text{шара}}^2\). Подставим найденное значение \(R_{\text{шара}}\): \(S_{\text{шара}} = 4\pi \left(\frac{H^2 + r^2}{2H}\right)^2\). Возведем дробь в квадрат: \(S_{\text{шара}} = 4\pi \frac{(H^2 + r^2)^2}{(2H)^2} = 4\pi \frac{(H^2 + r^2)^2}{4H^2}\). Сокращая \(4\) в числителе и знаменателе, получаем формулу для площади поверхности шара: \(S_{\text{шара}} = \frac{\pi (H^2 + r^2)^2}{H^2}\).
Далее найдем объём шара. Объём шара находится по формуле \(V_{\text{шара}} = \frac{4}{3}\pi R_{\text{шара}}^3\). Подставим найденное значение \(R_{\text{шара}}\): \(V_{\text{шара}} = \frac{4}{3}\pi \left(\frac{H^2 + r^2}{2H}\right)^3\). Возведем дробь в куб: \(V_{\text{шара}} = \frac{4}{3}\pi \frac{(H^2 + r^2)^3}{(2H)^3} = \frac{4}{3}\pi \frac{(H^2 + r^2)^3}{8H^3}\). Перемножим коэффициенты: \(V_{\text{шара}} = \frac{4\pi (H^2 + r^2)^3}{3 \cdot 8H^3} = \frac{4\pi (H^2 + r^2)^3}{24H^3}\). Сокращая \(4\) в числителе и знаменателе, получаем формулу для объёма шара: \(V_{\text{шара}} = \frac{\pi (H^2 + r^2)^3}{6H^3}\).
Таким образом, площадь поверхности шара равна \(S_{\text{шара}} = \frac{\pi (H^2 + r^2)^2}{H^2}\), а объём шара равен \(V_{\text{шара}} = \frac{\pi (H^2 + r^2)^3}{6H^3}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.