Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 550 Атанасян — Подробные Ответы
В сферу радиуса \(R\) вписан цилиндр, диагональ осевого сечения которого составляет с основанием угол \(\alpha\). Найдите объём цилиндра.
По теореме синусов в \(\triangle CDO\) имеем \(\frac{l}{\sin a} = \frac{R_{\text{ш}}}{\sin\left(\frac{180^\circ — a}{2}\right)} = \frac{R_{\text{ш}}}{\cos\frac{a}{2}}\), откуда находим радиус шара \(R_{\text{ш}} = \frac{l \cdot \cos\frac{a}{2}}{\sin a} = \frac{l \cdot \cos\frac{a}{2}}{2 \cdot \cos\frac{a}{2} \cdot \sin\frac{a}{2}} = \frac{l}{2 \cdot \sin\frac{a}{2}}\). Объем шара вычисляется по формуле \(V = \frac{4}{3}\pi \cdot R^3\). Подставляя найденное значение радиуса, получаем \(V = \frac{4}{3}\pi \cdot \left(\frac{l}{2 \cdot \sin\frac{a}{2}}\right)^3 = \frac{4\pi}{3} \cdot \frac{l^3}{8 \cdot \sin^3\frac{a}{2}} = \frac{\pi l^3}{6 \cdot \sin^3\frac{a}{2}}\). Ответ: \(V_{\text{шара}} = \frac{\pi l^3}{6 \cdot \sin^3\frac{a}{2}}\).
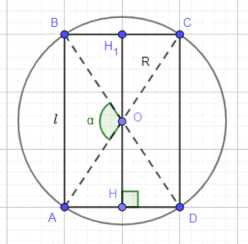
Дано: Шар с центром \(O\), вписанный цилиндр, осевое сечение цилиндра \(ADBC\), угол \(\angle BOA = a\), длина отрезка \(AB = l\). Найти: Объем шара \(V_{\text{шара}}\).
Решение:
Первый шаг: Высота цилиндра обозначена как \(HH_1\). Углы \(\angle BOA\) и \(\angle COD\) равны \(a\).
Второй шаг: Диагонали осевого сечения цилиндра \(AC\) и \(BD\) равны удвоенному радиусу сферы \(2R_{\text{сф}}\). Поскольку \(ADBC\) является осевым сечением вписанного цилиндра, его вершины лежат на сфере. Так как это осевое сечение, оно является прямоугольником.
Третий шаг: Рассмотрим треугольник \(CDO\). По теореме синусов для этого треугольника отношение стороны к синусу противолежащего угла равно удвоенному радиусу описанной окружности. В данном случае, описанной окружностью для треугольника \(CDO\) является большое окружность сферы, и ее радиус равен радиусу сферы \(R_{\text{ш}}\). Сторона \(CD\) равна \(l\). Угол \(\angle COD = a\). Углы \(\angle OCD\) и \(\angle ODC\) равны как углы при основании равнобедренного треугольника \(CDO\) (\(OC=OD=R_{\text{ш}}\)). Сумма углов в треугольнике \(CDO\) равна \(180^\circ\), следовательно \(\angle OCD = \angle ODC = \frac{180^\circ — a}{2}\). Применяя теорему синусов к стороне \(CD\) и углу \(\angle COD\), а также к стороне \(OD\) (или \(OC\)) и углу \(\angle OCD\) (или \(\angle ODC\)), получаем соотношение \(\frac{l}{\sin a} = \frac{R_{\text{ш}}}{\sin\left(\frac{180^\circ — a}{2}\right)}\). Учитывая, что \(\sin\left(\frac{180^\circ — a}{2}\right) = \sin\left(90^\circ — \frac{a}{2}\right) = \cos\frac{a}{2}\), получаем \(\frac{l}{\sin a} = \frac{R_{\text{ш}}}{\cos\frac{a}{2}}\). Из этого уравнения выразим радиус шара \(R_{\text{ш}}\): \(R_{\text{ш}} = \frac{l \cdot \cos\frac{a}{2}}{\sin a}\). Используя формулу синуса двойного угла \(\sin a = 2 \sin\frac{a}{2} \cos\frac{a}{2}\), преобразуем выражение для \(R_{\text{ш}}\): \(R_{\text{ш}} = \frac{l \cdot \cos\frac{a}{2}}{2 \cdot \cos\frac{a}{2} \cdot \sin\frac{a}{2}} = \frac{l}{2 \cdot \sin\frac{a}{2}}\).
Четвертый шаг: Найдем объем шара. Объем шара вычисляется по формуле \(V = \frac{4}{3}\pi R^3\), где \(R\) — радиус шара. Подставим найденное значение радиуса \(R_{\text{ш}}\) в формулу объема: \(V_{\text{шара}} = \frac{4}{3}\pi \cdot \left(\frac{l}{2 \cdot \sin\frac{a}{2}}\right)^3\). Возведем в куб выражение в скобках: \(\left(\frac{l}{2 \cdot \sin\frac{a}{2}}\right)^3 = \frac{l^3}{2^3 \cdot \sin^3\frac{a}{2}} = \frac{l^3}{8 \cdot \sin^3\frac{a}{2}}\). Теперь подставим это обратно в формулу объема: \(V_{\text{шара}} = \frac{4}{3}\pi \cdot \frac{l^3}{8 \cdot \sin^3\frac{a}{2}}\). Сократим числитель и знаменатель: \(V_{\text{шара}} = \frac{4\pi l^3}{24 \cdot \sin^3\frac{a}{2}} = \frac{\pi l^3}{6 \cdot \sin^3\frac{a}{2}}\).
Таким образом, объем шара равен \(\frac{\pi l^3}{6 \cdot \sin^3\frac{a}{2}}\).
Ответ: \(\frac{\pi l^3}{6 \cdot \sin^3\frac{a}{2}}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.