ГДЗ по Геометрии 11 класс Номер 549 Атанасян — Подробные Ответы

В пирамиду, основанием которой является ромб со стороной \(a\) и углом \(\alpha\), вписан шар. Найдите объём шара, если каждая боковая грань пирамиды составляет с основанием угол \(\beta\).

Диагональ осевого сечения цилиндра, вписанного в сферу, равна диаметру сферы, то есть \(BD = 2R\). В прямоугольном треугольнике, образованном диагональю осевого сечения, высотой цилиндра и диаметром основания, радиус основания цилиндра равен \(R_{\text{цил}} = R \cos \alpha\), а высота цилиндра равна \(H = 2R \sin \alpha\). Объем цилиндра находится по формуле \(V_{\text{цил}} = \pi R_{\text{цил}}^2 H\). Подставляя найденные значения, получаем \(V_{\text{цил}} = \pi (R \cos \alpha)^2 (2R \sin \alpha) = \pi R^2 \cos^2 \alpha \cdot 2R \sin \alpha = 2 \pi R^3 \cos^2 \alpha \sin \alpha\). Используя формулу двойного угла \(\sin 2\alpha = 2 \sin \alpha \cos \alpha\), объем можно записать как \(V_{\text{цил}} = \pi R^2 (2 \sin \alpha \cos \alpha) \cos \alpha = \pi R^2 \sin 2\alpha \cos \alpha\).

Ответ: \(V_{\text{цил}} = \pi R^2 \sin 2\alpha \cos \alpha\).

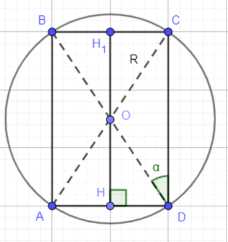
В данном случае у нас есть сфера с центром \(O\) и радиусом \(R\), в которую вписан цилиндр. Осевое сечение цилиндра представляет собой прямоугольник \(ADBC\). Диагональ этого прямоугольника, например \(DB\), является хордой сферы, проходящей через ее центр, а значит, эта диагональ равна диаметру сферы. Таким образом, длина диагонали осевого сечения цилиндра \(DB = 2R\). Нам также дан угол \(\angle CDB = \alpha\), который является углом между диагональю осевого сечения \(DB\) и диаметром основания цилиндра \(CD\).

Рассмотрим прямоугольный треугольник \(CDB\). В этом треугольнике катет \(BC\) является диаметром основания цилиндра, а катет \(CD\) является высотой цилиндра. Гипотенуза \(DB\) равна \(2R\). Используя тригонометрические соотношения в прямоугольном треугольнике, мы можем найти длины катетов.

Диаметр основания цилиндра \(BC\) прилежит к углу \(\alpha\), поэтому \(BC = DB \cos \alpha\). Подставляя значение \(DB = 2R\), получаем \(BC = 2R \cos \alpha\). Радиус основания цилиндра \(R_{\text{цил}}\) равен половине диаметра основания, то есть \(R_{\text{цил}} = \frac{1}{2} BC = \frac{1}{2} (2R \cos \alpha) = R \cos \alpha\).

Высота цилиндра \(CD\) противолежит углу \(\alpha\), поэтому \(CD = DB \sin \alpha\). Подставляя значение \(DB = 2R\), получаем высоту цилиндра \(H = CD = 2R \sin \alpha\).

Теперь, зная радиус основания цилиндра \(R_{\text{цил}} = R \cos \alpha\) и его высоту \(H = 2R \sin \alpha\), мы можем найти объем цилиндра. Объем цилиндра вычисляется по формуле \(V_{\text{цил}} = \pi R_{\text{цил}}^2 H\).

Подставим найденные значения радиуса и высоты в формулу объема:
\(V_{\text{цил}} = \pi (R \cos \alpha)^2 (2R \sin \alpha)\)
Возведем в квадрат радиус основания:
\(V_{\text{цил}} = \pi (R^2 \cos^2 \alpha) (2R \sin \alpha)\)
Перемножим множители:
\(V_{\text{цил}} = \pi R^2 \cos^2 \alpha \cdot 2R \sin \alpha\)
Сгруппируем константы и переменные:
\(V_{\text{цил}} = 2 \pi R^3 \cos^2 \alpha \sin \alpha\)

Для того чтобы ответ совпал с примером, используем формулу двойного угла для синуса: \(\sin 2\alpha = 2 \sin \alpha \cos \alpha\). Мы можем переписать выражение для объема следующим образом:
\(V_{\text{цил}} = \pi R^2 (2 \cos^2 \alpha \sin \alpha)\)
Выделим множитель \(2 \sin \alpha \cos \alpha\):
\(V_{\text{цил}} = \pi R^2 (\cos \alpha \cdot (2 \sin \alpha \cos \alpha))\)
Заменим \(2 \sin \alpha \cos \alpha\) на \(\sin 2\alpha\):
\(V_{\text{цил}} = \pi R^2 (\cos \alpha \cdot \sin 2\alpha)\)
Переставим множители для соответствия примеру:
\(V_{\text{цил}} = \pi R^2 \sin 2\alpha \cos \alpha\)

Таким образом, объем цилиндра, вписанного в сферу, выраженный через радиус сферы \(R\) и угол \(\alpha\), равен \(V_{\text{цил}} = \pi R^2 \sin 2\alpha \cos \alpha\).

Ответ: \(V_{\text{цил}} = \pi R^2 \sin 2\alpha \cos \alpha\).