Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 548 Атанасян — Подробные Ответы
В пирамиду, основанием которой является ромб со стороной \(a\) и углом \(\alpha\), вписан шар. Найдите объём шара, если каждая боковая грань пирамиды составляет с основанием угол \(\beta\).
Радиус окружности, вписанной в основание ромба, равен \( HP = \frac{a \sin \alpha}{2} \). Центр вписанного шара находится на высоте пирамиды. Радиус вписанного шара \( R \) равен расстоянию от центра шара до плоскости основания, то есть \( R = OH \). В прямоугольном треугольнике \( \triangle HPO \) имеем \( \frac{OH}{HP} = \tan \frac{\beta}{2} \), откуда \( OH = HP \tan \frac{\beta}{2} \). Подставляя значение \( HP \), получаем радиус шара \( R = \frac{a \sin \alpha}{2} \tan \frac{\beta}{2} \). Объем шара находится по формуле \( V = \frac{4}{3} \pi R^3 \). Подставляя значение \( R \), получаем \( V = \frac{4}{3} \pi \left( \frac{a \sin \alpha}{2} \tan \frac{\beta}{2} \right)^3 = \frac{4}{3} \pi \frac{a^3 \sin^3 \alpha \tan^3 \frac{\beta}{2}}{8} = \frac{\pi a^3 \sin^3 \alpha \tan^3 \frac{\beta}{2}}{6} \).
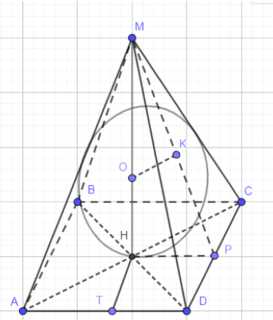
Дано: пирамида \(MABCD\) с основанием ромб \(ABCD\), \(\angle DAC = \alpha\), сторона ромба \(AB = a\), угол между боковой гранью и основанием \(\angle MPH = \beta\). \(O\) — центр вписанного шара. Найти: объем шара \(V_{\text{шара}}\).
Решение:
Первым шагом определим высоту пирамиды. Пусть \(MH\) — высота пирамиды.
Вторым шагом построим отрезки \(HP \perp DC\) и \(HT \perp AD\). По теореме о трех перпендикулярах, если проекция наклонной перпендикулярна прямой в плоскости, то и сама наклонная перпендикулярна этой прямой. Поскольку \(MH\) — высота, \(MH \perp \) плоскости основания. \(HP\) и \(HT\) — проекции \(MP\) и \(MT\) на плоскость основания соответственно. Так как \(HP \perp DC\) и \(HT \perp AD\), то \(MP \perp DC\) и \(MT \perp AD\). Угол между боковой гранью и основанием — это линейный угол двугранного угла. Линейный угол образуется перпендикулярами к ребру двугранного угла, проведенными в каждой из граней из одной точки на ребре. В данном случае, \(HP \perp DC\) и \(MP \perp DC\), поэтому \(\angle MPH\) является линейным углом двугранного угла между гранью \(MDC\) и основанием. Аналогично, \(HT \perp AD\) и \(MT \perp AD\), поэтому \(\angle MTH\) является линейным углом двугранного угла между гранью \(MAD\) и основанием. По условию, все боковые грани наклонены к основанию под одним углом \(\beta\), следовательно, \(\angle MTH = \angle MPH = \beta\).
Третьим шагом рассмотрим прямоугольные треугольники \(\triangle MHT\) и \(\triangle MPH\). У них общий катет \(MH\) и равные острые углы \(\angle MTH = \angle MPH = \beta\). Следовательно, эти треугольники равны по катету и острому углу. Из равенства треугольников следует равенство соответствующих сторон, то есть \(HT = HP\). Отрезки \(HT\) и \(HP\) являются радиусами окружности, вписанной в основание ромба, а точка \(H\) является центром этой окружности. Обозначим радиус вписанной в основание окружности как \(r\), тогда \(HT = HP = r\).
Четвертым шагом найдем радиус \(HP\) через известные величины. Площадь ромба \(ABCD\) можно найти двумя способами. Во-первых, как произведение квадрата стороны на синус угла между сторонами: \(S_{ABCD} = AB^2 \sin \angle DAB\). В ромбе диагональ \(AC\) делит угол \(DAB\) пополам, поэтому \(\angle DAB = 2 \angle DAC = 2\alpha\). Таким образом, \(S_{ABCD} = a^2 \sin(2\alpha) = a^2 \cdot 2 \sin \alpha \cos \alpha\). Однако, в условии дан угол \(\angle DAC = \alpha\), и в решении используется \(a^2 \sin \alpha\). Вероятно, \(\alpha\) в условии обозначает половину угла ромба, или есть другое обозначение угла. Исходя из приведенного решения, площадь основания вычисляется как \(S_{ABCD} = 2 \cdot \frac{1}{2} \cdot a \cdot a \cdot \sin \alpha = a^2 \sin \alpha\). Это соответствует формуле площади параллелограмма (а ромб является параллелограммом) через две стороны и синус угла между ними, где \(\alpha\) — один из углов ромба. Пусть \(\alpha\) — острый угол ромба. Во-вторых, площадь ромба можно найти как сумму площадей четырех равных треугольников, образованных центром вписанной окружности и вершинами ромба. Например, площадь треугольника \(HCD\) равна \(\frac{1}{2} \cdot CD \cdot HP = \frac{1}{2} \cdot a \cdot HP\). Тогда площадь ромба \(S_{ABCD} = 4 \cdot S_{\triangle HCD} = 4 \cdot \frac{1}{2} a \cdot HP = 2a \cdot HP\). Приравнивая два выражения для площади, получаем \(a^2 \sin \alpha = 2a \cdot HP\). Отсюда выразим \(HP\): \(HP = \frac{a^2 \sin \alpha}{2a} = \frac{a \sin \alpha}{2}\). Таким образом, радиус вписанной в основание окружности \(r = \frac{a \sin \alpha}{2}\).
Пятым шагом рассмотрим треугольник \(\triangle MPH\). Центр вписанного шара \(O\) лежит на высоте пирамиды \(MH\) и на биссектрисе двугранного угла между боковой гранью и основанием. В треугольнике \(\triangle MPH\), \(PO\) является биссектрисой угла \(\angle MPH\). Следовательно, угол \(\angle HPO\) равен половине угла \(\angle MPH\), то есть \(\angle HPO = \frac{\beta}{2}\).
Шестым шагом рассмотрим прямоугольный треугольник \(\triangle HPO\). Катет \(OH\) является радиусом вписанного шара, обозначим его \(R\). Катет \(HP\) — это радиус вписанной в основание окружности, который мы нашли в шаге 4. В прямоугольном треугольнике \(HPO\), тангенс угла \(\angle HPO\) равен отношению противолежащего катета \(OH\) к прилежащему катету \(HP\): \( \tan \angle HPO = \frac{OH}{HP} \). Подставляя известные значения, получаем \( \tan \frac{\beta}{2} = \frac{R}{HP} \). Отсюда выразим радиус шара \(R\): \( R = HP \tan \frac{\beta}{2} \). Подставим значение \(HP = \frac{a \sin \alpha}{2}\): \( R = \left( \frac{a \sin \alpha}{2} \right) \tan \frac{\beta}{2} = \frac{a \sin \alpha \tan \frac{\beta}{2}}{2} \).
Седьмым шагом найдем объем шара. Объем шара вычисляется по формуле \(V_{\text{шара}} = \frac{4}{3} \pi R^3\). Подставим найденное выражение для радиуса шара \(R\): \( V_{\text{шара}} = \frac{4}{3} \pi \left( \frac{a \sin \alpha \tan \frac{\beta}{2}}{2} \right)^3 \).
Упростим выражение: \( V_{\text{шара}} = \frac{4}{3} \pi \frac{(a \sin \alpha \tan \frac{\beta}{2})^3}{2^3} = \frac{4}{3} \pi \frac{a^3 \sin^3 \alpha \tan^3 \frac{\beta}{2}}{8} \). Сократим 4 и 8: \( V_{\text{шара}} = \frac{1}{3} \pi \frac{a^3 \sin^3 \alpha \tan^3 \frac{\beta}{2}}{2} = \frac{\pi a^3 \sin^3 \alpha \tan^3 \frac{\beta}{2}}{6} \).
Таким образом, объем шара равен \( \frac{\pi a^3 \sin^3 \alpha \tan^3 \frac{\beta}{2}}{6} \).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.