
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 547 Атанасян — Подробные Ответы
В правильную треугольную пирамиду с двугранным углом \(\alpha\) при основании вписан шар объёма \(V\). Найдите объём пирамиды.
Из объема шара \(V = \frac{4}{3}\pi R^3\) находим куб радиуса вписанного шара \(R^3 = \frac{3V}{4\pi}\). Радиус вписанной в основание окружности \(r = \frac{R}{\tan(\alpha/2)}\). Высота пирамиды \(H = r \tan \alpha = \frac{R \tan \alpha}{\tan(\alpha/2)}\). Сторона основания \(a = r \cdot 2\sqrt{3} = \frac{2\sqrt{3}R}{\tan(\alpha/2)}\). Площадь основания \(S = \frac{a^2\sqrt{3}}{4} = \frac{(2\sqrt{3}R/\tan(\alpha/2))^2\sqrt{3}}{4} = \frac{12R^2\sqrt{3}}{4\tan^2(\alpha/2)} = \frac{3\sqrt{3}R^2}{\tan^2(\alpha/2)}\). Объем пирамиды \(V_{\text{пир}} = \frac{1}{3}SH = \frac{1}{3} \frac{3\sqrt{3}R^2}{\tan^2(\alpha/2)} \frac{R \tan \alpha}{\tan(\alpha/2)} = \frac{\sqrt{3}R^3 \tan \alpha}{\tan^3(\alpha/2)}\). Подставляя \(R^3 = \frac{3V}{4\pi}\), получаем \(V_{\text{пир}} = \frac{\sqrt{3} \frac{3V}{4\pi} \tan \alpha}{\tan^3(\alpha/2)} = \frac{3\sqrt{3}V \tan \alpha}{4\pi \tan^3(\alpha/2)} = \frac{3\sqrt{3}}{4\pi} \tan \alpha \cot^3 \frac{\alpha}{2} V\).
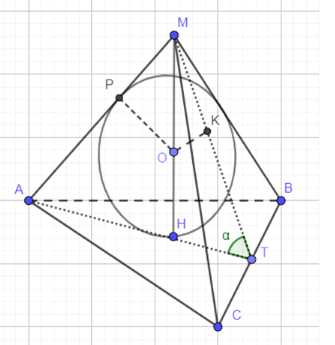
Дано правильная треугольная пирамида МАВС, где \(\angle MTA = \alpha\) является линейным углом двугранного угла при основании, О — центр вписанного шара, V — объем вписанного шара. Требуется найти объем пирамиды \(V_{\text{пирамиды}}\).
Объем вписанного шара выражается формулой \(V = \frac{4}{3}\pi R^3\), где \(R\) обозначает радиус этого шара. Из данного соотношения мы можем выразить куб радиуса шара: \(R^3 = \frac{3V}{4\pi}\).
Радиус вписанной в основание окружности, который также является апофемой основания правильной треугольной пирамиды, обозначим через \(r\). Существует связь между радиусом вписанного шара \(R\), радиусом вписанной в основание окружности \(r\) и линейным углом двугранного угла при основании \(\alpha\), которая выражается формулой \(r = R \cot(\alpha/2)\).
Основание пирамиды представляет собой правильный треугольник. Для правильного треугольника со стороной \(a\), радиус вписанной окружности \(r\) связан со стороной соотношением \(r = \frac{a}{2\sqrt{3}}\). Из этого следует, что сторона основания \(a = 2\sqrt{3}r\). Подставляя выражение для \(r\), получаем \(a = 2\sqrt{3}R \cot(\alpha/2)\).
Высота пирамиды \(H\) связана с апофемой основания \(r\) и линейным углом \(\alpha\) соотношением \(H = r \tan \alpha\). Подставляя выражение для \(r\), находим высоту пирамиды: \(H = R \cot(\alpha/2) \tan \alpha\). Используя тригонометрическое тождество \(\cot(\alpha/2) = \frac{1}{\tan(\alpha/2)}\), это можно записать как \(H = \frac{R \tan \alpha}{\tan(\alpha/2)}\).
Площадь основания правильного треугольника со стороной \(a\) вычисляется по формуле \(S_{\text{осн}} = \frac{\sqrt{3}}{4}a^2\). Подставляя найденное выражение для стороны основания \(a\), получаем \(S_{\text{осн}} = \frac{\sqrt{3}}{4}(2\sqrt{3}R \cot(\alpha/2))^2 = \frac{\sqrt{3}}{4}(12R^2 \cot^2(\alpha/2)) = 3\sqrt{3}R^2 \cot^2(\alpha/2)\).
Объем пирамиды определяется формулой \(V_{\text{пир}} = \frac{1}{3} S_{\text{осн}} \cdot H\). Подставляя полученные выражения для площади основания и высоты пирамиды, имеем \(V_{\text{пир}} = \frac{1}{3} (3\sqrt{3}R^2 \cot^2(\alpha/2)) (R \cot(\alpha/2) \tan \alpha) = \sqrt{3}R^3 \cot^3(\alpha/2) \tan \alpha\).
Наконец, подставляем выражение для \(R^3\) через объем шара V: \(V_{\text{пир}} = \sqrt{3} \left(\frac{3V}{4\pi}\right) \cot^3(\alpha/2) \tan \alpha = \frac{3\sqrt{3}V}{4\pi} \cot^3(\alpha/2) \tan \alpha\).
Таким образом, объем пирамиды равен \(\frac{3\sqrt{3}}{4\pi} \tan \alpha \cot^3 \frac{\alpha}{2} V\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!