Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 546 Атанасян — Подробные Ответы
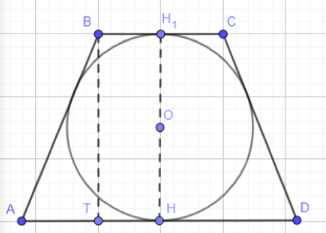
В усечённый конус, радиусы оснований которого равны \(r\) и \(r_1\), вписан шар. Найдите отношение объёмов усечённого конуса и шара.
Высота усеченного конуса равна диаметру вписанного шара, то есть \(HH_1 = 2R\), где \(R\) — радиус шара. Осевое сечение конуса — равнобокая трапеция, описанная около окружности. По свойству описанного четырехугольника, сумма оснований равна сумме боковых сторон. Основания трапеции равны \(2r\) и \(2r_1\), боковые стороны равны \(AB\) и \(CD\). Так как трапеция равнобокая, \(AB = CD\). Значит, \(2r + 2r_1 = 2AB\), откуда \(AB = r + r_1\). Высота трапеции \(BT\) равна \(HH_1\). В прямоугольном треугольнике \(ABT\), по теореме Пифагора, \(BT^2 = AB^2 — AT^2\). \(AT = \frac{2r_1 — 2r}{2} = r_1 — r\) (если \(r_1 > r\)) или \(r — r_1\) (если \(r > r_1\)). В любом случае \(AT^2 = (r_1 — r)^2\). Тогда \((2R)^2 = (r+r_1)^2 — (r_1-r)^2\). Упрощая правую часть: \((r+r_1)^2 — (r_1-r)^2 = (r^2 + 2rr_1 + r_1^2) — (r_1^2 — 2rr_1 + r^2) = 4rr_1\). Следовательно, \(4R^2 = 4rr_1\), откуда \(R^2 = rr_1\), и \(R = \sqrt{rr_1}\). Объем усеченного конуса равен \(V_{конуса} = \frac{1}{3}\pi HH_1 (r^2 + r_1^2 + rr_1) = \frac{1}{3}\pi (2R) (r^2 + r_1^2 + rr_1) =\)
\(= \frac{2}{3}\pi R (r^2 + r_1^2 + rr_1)\). Объем шара равен \(V_{шара} = \frac{4}{3}\pi R^3\). Отношение объемов: \(\frac{V_{конуса}}{V_{шара}} = \frac{\frac{2}{3}\pi R (r^2 + r_1^2 + rr_1)}{\frac{4}{3}\pi R^3} = \frac{2R (r^2 + r_1^2 + rr_1)}{4R^3} = \frac{r^2 + r_1^2 + rr_1}{2R^2}\). Подставляя \(R^2 = rr_1\), получаем \(\frac{r^2 + r_1^2 + rr_1}{2rr_1}\).
Дано: усеченный конус с радиусами оснований \(r\) (верхнее основание) и \(r_1\) (нижнее основание). В конус вписан шар с центром \(O\).
Найти: отношение объема конуса к объему шара, то есть \(\frac{V_{конуса}}{V_{шара}}\).
Решение:
Сначала определим высоту усеченного конуса. Поскольку в усеченный конус вписан шар, высота конуса \(HH_1\) равна диаметру этого шара. Если \(R\) — радиус шара, то высота конуса \(HH_1 = 2R\). Осевое сечение усеченного конуса, в который вписан шар, представляет собой равнобокую трапецию \(BCDA\), описанную около окружности (большого круга шара).
Объем усеченного конуса вычисляется по формуле \(V_{конуса} = \frac{1}{3}\pi h (r_{верх}^2 + r_{ниж}^2 + r_{верх} r_{ниж})\), где \(h\) — высота конуса, \(r_{верх}\) и \(r_{ниж}\) — радиусы оснований. В нашем случае \(h = HH_1 = 2R\), \(r_{верх} = r\), \(r_{ниж} = r_1\). Подставляя эти значения, получаем \(V_{конуса} = \frac{1}{3}\pi (2R) (r^2 + r_1^2 + rr_1) = \frac{2}{3}\pi R (r^2 + r_1^2 + rr_1)\).
Рассмотрим осевое сечение \(ABCD\). Это трапеция с основаниями \(AD = 2r\) и \(BC = 2r_1\) и боковыми сторонами \(AB\) и \(CD\). Поскольку трапеция описана около окружности, сумма длин противоположных сторон равна: \(AD + BC = AB + CD\). Так как трапеция равнобокая, \(AB = CD\). Следовательно, \(2r + 2r_1 = 2AB\), откуда \(AB = r + r_1\).
Построим высоту \(BT\) из вершины \(B\) на основание \(AD\). \(BT\) перпендикулярна \(AD\) и параллельна \(HH_1\). Длина \(BT\) равна высоте конуса, то есть \(BT = HH_1 = 2R\). Отрезок \(AT\) равен полуразности оснований трапеции: \(AT = \frac{AD — BC}{2} = \frac{2r_1 — 2r}{2} = r_1 — r\) (предполагая \(r_1 > r\)). Если \(r > r_1\), то \(AT = r — r_1\). В любом случае, \(AT^2 = (r_1 — r)^2\).
Рассмотрим прямоугольный треугольник \(ABT\). По теореме Пифагора, \(AB^2 = BT^2 + AT^2\). Подставим известные значения: \((r + r_1)^2 = (2R)^2 + (r_1 — r)^2\). Раскроем скобки: \(r^2 + 2rr_1 + r_1^2 = 4R^2 + r_1^2 — 2rr_1 + r^2\). Перенесем все члены, кроме \(4R^2\), в левую часть: \(r^2 + 2rr_1 + r_1^2 — r_1^2 + 2rr_1 — r^2 = 4R^2\). Упрощая, получаем \(4rr_1 = 4R^2\), откуда \(R^2 = rr_1\). Радиус шара равен \(R = \sqrt{rr_1}\).
Теперь найдем отношение объемов конуса и шара. Объем шара равен \(V_{шара} = \frac{4}{3}\pi R^3\). Отношение объемов равно \(\frac{V_{конуса}}{V_{шара}} = \frac{\frac{2}{3}\pi R (r^2 + r_1^2 + rr_1)}{\frac{4}{3}\pi R^3}\). Сократим общие множители: \(\frac{2R (r^2 + r_1^2 + rr_1)}{4R^3} = \frac{r^2 + r_1^2 + rr_1}{2R^2}\). Подставим найденное значение \(R^2 = rr_1\): \(\frac{r^2 + r_1^2 + rr_1}{2rr_1}\).
Таким образом, отношение объемов усеченного конуса и вписанного шара равно \(\frac{r^2 + r_1^2 + rr_1}{2rr_1}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.