ГДЗ по Геометрии 11 класс Номер 545 Атанасян — Подробные Ответы

В конус, радиус основания которого равен \(r\), а образующая равна \(l\), вписана сфера. Найдите длину линии, по которой сфера касается боковой поверхности конуса.

Рассмотрим осевое сечение конуса и вписанной сферы. Сфера касается образующей конуса в некоторой точке. Расстояние от вершины конуса до этой точки касания на образующей равно разности длины образующей и радиуса основания, то есть \(l-r\). Пусть \(r_c\) — радиус окружности касания сферы с боковой поверхностью конуса. Из подобия треугольников в осевом сечении следует, что отношение радиуса окружности касания к радиусу основания конуса равно отношению расстояния от вершины до точки касания на образующей к длине образующей. Таким образом, имеем \(\frac{r_c}{r} = \frac{l-r}{l}\). Отсюда находим радиус окружности касания: \(r_c = r \frac{l-r}{l}\). Длина окружности касания равна ее длине окружности, которая вычисляется по формуле \(c = 2\pi r_c\). Подставляя выражение для \(r_c\), получаем \(c = 2\pi r \frac{l-r}{l}\).

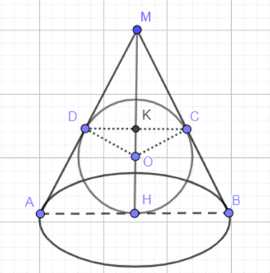
Рассмотрим осевое сечение данного конуса. В сечении мы получим равнобедренный треугольник, основание которого равно диаметру основания конуса \(2r\), а боковые стороны равны образующей конуса \(l\). В это треугольник вписана окружность, являющаяся осевым сечением сферы. Центр этой окружности лежит на высоте конуса. Точки касания сферы с конусом образуют окружность на боковой поверхности конуса. В осевом сечении эта окружность касания представлена точкой D на образующей MA.

По свойству касательных, проведенных из одной точки к окружности, отрезки касательных равны. В нашем случае, из вершины A к вписанной в треугольник окружности проведены касательные AH и AD. Следовательно, длина отрезка AD равна длине отрезка AH, который является радиусом основания конуса. Таким образом, \(AD = AH = r\).

Длина образующей конуса MA равна \(l\). Точка D лежит на образующей MA. Длина отрезка MD равна разности длины всей образующей MA и длины отрезка AD. Следовательно, \(MD = MA — AD = l — r\).

Теперь рассмотрим прямоугольный треугольник MAH, где MH — высота конуса, AH — радиус основания, MA — образующая. В осевом сечении, проведем перпендикуляр из точки D к высоте конуса MH. Основание этого перпендикуляра обозначим K. Отрезок DK является радиусом окружности касания сферы с боковой поверхностью конуса. Треугольник MDK является прямоугольным с прямым углом при вершине K.

Треугольник MDK подобен прямоугольному треугольнику MAH. У них общий угол при вершине M (\(\angle DMK = \angle AMH\)), и оба треугольника прямоугольные (\(\angle MKB = \angle MHA = 90^\circ\)).

Из подобия треугольников MDK и MAH следует пропорциональность их соответствующих сторон. Отношение радиуса окружности касания DK к радиусу основания конуса AH равно отношению отрезка MD к образующей конуса MA. Запишем это соотношение: \(\frac{DK}{AH} = \frac{MD}{MA}\).

Подставим известные значения: \(AH = r\), \(MA = l\), \(MD = l — r\). Получим: \(\frac{DK}{r} = \frac{l-r}{l}\).

Выразим радиус окружности касания DK из этого уравнения: \(DK = r \cdot \frac{l-r}{l}\). Это и есть радиус окружности, по которой сфера касается боковой поверхности конуса.

Нам необходимо найти длину этой окружности касания. Длина окружности вычисляется по формуле \(c = 2\pi \cdot \text{радиус}\). В данном случае, радиус равен DK.

Следовательно, длина окружности касания равна \(c = 2\pi \cdot DK = 2\pi \cdot \left(r \frac{l-r}{l}\right)\).

Окончательно получаем формулу для длины линии касания: \(c = 2\pi r \frac{l-r}{l}\).