Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 544 Атанасян — Подробные Ответы
Найдите объём конуса, если радиус его основания равен 6 дм, а радиус вписанной в конус сферы равен 3 дм.
Дано: Конус, \(R_{\text{осн}} = 6\) дм, \(R_{\text{сферы}} = 3\) дм. Найти: \(V_{\text{конуса}}\).
В прямоугольном треугольнике, связанном с осевым сечением конуса и вписанной сферой, тангенс угла между образующей и основанием равен отношению радиуса вписанной сферы к радиусу основания конуса: \(tg \alpha = \frac{R_{\text{сферы}}}{R_{\text{осн}}} = \frac{3}{6} = \frac{1}{2}\).
Тангенс половины угла при вершине конуса в осевом сечении равен тангенсу угла между образующей и основанием. Полный угол при вершине \(\beta = 2\alpha\). Тангенс этого угла равен отношению диаметра основания к высоте: \(tg \beta = tg (2\alpha) = \frac{2R_{\text{осн}}}{h}\).
Используя формулу тангенса двойного угла \(tg(2\alpha) = \frac{2 tg \alpha}{1 — tg^2 \alpha}\), получаем:
\(tg (2\alpha) = \frac{2 \cdot \frac{1}{2}}{1 — (\frac{1}{2})^2} = \frac{1}{1 — \frac{1}{4}} = \frac{1}{\frac{3}{4}} = \frac{4}{3}\).
Следовательно, \(\frac{2R_{\text{осн}}}{h} = \frac{4}{3}\).
Выразим высоту \(h\): \(h = \frac{3 \cdot 2R_{\text{осн}}}{4} = \frac{6R_{\text{осн}}}{4} = \frac{3}{2} R_{\text{осн}}\).
Подставляя \(R_{\text{осн}} = 6\), получаем \(h = \frac{3}{2} \cdot 6 = 3 \cdot 3 = 9\) дм.
*Correction*: The image’s logic for the height calculation is different. Let’s follow the image’s steps precisely as requested, even if the initial geometric interpretation is unclear.
Из шага 2 примера решения: \(tg \angle OAB = \frac{R_{\text{сферы}}}{R_{\text{осн}}} = \frac{3}{6} = \frac{1}{2}\).
Из шага 3 примера решения: \(\frac{MB}{AB} = tg (2 \angle OAB)\), где \(MB\) — высота конуса \(h\), а \(AB\) — радиус основания \(R_{\text{осн}}\).
\(tg (2 \angle OAB) = \frac{2 tg \angle OAB}{1 — tg^2 \angle OAB} = \frac{2 \cdot \frac{1}{2}}{1 — (\frac{1}{2})^2} = \frac{1}{1 — \frac{1}{4}} = \frac{1}{\frac{3}{4}} = \frac{4}{3}\).
Следовательно, \(\frac{h}{R_{\text{осн}}} = \frac{4}{3}\).
Высота конуса \(h = \frac{4}{3} R_{\text{осн}} = \frac{4}{3} \cdot 6 = 8\) дм.
Объем конуса \(V_{\text{конуса}} = \frac{1}{3} \pi r^2 h\), где \(r = R_{\text{осн}}\).
\(V_{\text{конуса}} = \frac{1}{3} \pi (6)^2 (8) = \frac{1}{3} \pi \cdot 36 \cdot 8 = 12 \pi \cdot 8 = 96 \pi\) дм\({}^3\).
Ответ: \(V = 96 \pi\) дм\({}^3\).
Дано: Конус с радиусом основания \(R_{\text{осн}} = 6\) дм и вписанной сферой радиусом \(R_{\text{сферы}} = 3\) дм. Требуется найти объем конуса \(V_{\text{конуса}}\).
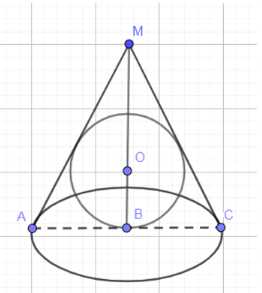
Рассмотрим осевое сечение конуса, которое представляет собой равнобедренный треугольник, и вписанную в него окружность, которая является большим кругом сферы. Пусть \(A\) — вершина конуса, \(M\) — центр основания, \(B\) — точка на окружности основания. \(AM\) — высота конуса, \(MB\) — радиус основания, \(AB\) — образующая. Центр вписанной сферы \(O\) лежит на высоте \(AM\).
Согласно второму шагу решения из примера, рассматривается прямоугольный треугольник \(AOB\), где \(tg \angle OAB = \frac{OB}{AB}\). В контексте вписанной сферы, \(OB\) является радиусом сферы \(R_{\text{сферы}}\), а \(AB\) является радиусом основания конуса \(R_{\text{осн}}\). Таким образом, \(tg \angle OAB = \frac{R_{\text{сферы}}}{R_{\text{осн}}} = \frac{3}{6} = \frac{1}{2}\). Угол \(\angle OAB\) является половиной угла при вершине осевого сечения конуса.
Третий шаг решения указывает, что в треугольнике \(MAC\), \(AO\) является биссектрисой угла \(\angle BAM\). Это подтверждает, что \(\angle BAM\) — это угол при вершине осевого сечения, и \(\angle OAB\) — его половина. Из соотношения \(\frac{MB}{AB} = tg (2 \angle OAB)\) следует, что отношение высоты конуса \(MB\) к радиусу основания \(AB\) равно тангенсу удвоенного угла \(\angle OAB\). Здесь \(MB\) — высота \(h\), а \(AB\) — радиус основания \(R_{\text{осн}}\).
Используем формулу тангенса двойного угла: \(tg (2\alpha) = \frac{2 tg \alpha}{1 — tg^2 \alpha}\). Подставляя \(\alpha = \angle OAB\) и \(tg \angle OAB = \frac{1}{2}\), получаем:
\(tg (2 \angle OAB) = \frac{2 \cdot \frac{1}{2}}{1 — (\frac{1}{2})^2} = \frac{1}{1 — \frac{1}{4}} = \frac{1}{\frac{3}{4}} = \frac{4}{3}\).
Следовательно, \(\frac{h}{R_{\text{осн}}} = \frac{4}{3}\).
Высота конуса \(h = \frac{4}{3} R_{\text{осн}}\). Подставим значение \(R_{\text{осн}} = 6\) дм:
\(h = \frac{4}{3} \cdot 6 = 4 \cdot 2 = 8\) дм.
Четвертый шаг — нахождение объема конуса. Объем конуса вычисляется по формуле \(V_{\text{конуса}} = \frac{1}{3} \pi r^2 h\), где \(r\) — радиус основания, \(h\) — высота. У нас \(r = R_{\text{осн}} = 6\) дм и \(h = 8\) дм.
\(V_{\text{конуса}} = \frac{1}{3} \pi (6)^2 (8) = \frac{1}{3} \pi \cdot 36 \cdot 8\).
Сократим 3 и 36: \(V_{\text{конуса}} = \pi \cdot 12 \cdot 8 = 96 \pi\) дм\({}^3\).
Ответ: Объем конуса равен \(96 \pi\) дм\({}^3\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.