ГДЗ по Геометрии 11 класс Номер 543 Атанасян — Подробные Ответы

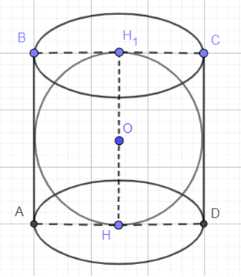
В цилиндр вписан шар. Найдите отношение объёмов цилиндра и шара.

Высота цилиндра равна диаметру вписанного шара, то есть \(h = 2R\), где \(R\) — радиус шара. Радиус основания цилиндра равен радиусу шара, то есть \(R_{\text{цил}} = R\). Объем цилиндра равен \(V_{\text{цил}} = \pi R_{\text{цил}}^2 h = \pi R^2 (2R) = 2\pi R^3\). Объем шара равен \(V_{\text{шара}} = \frac{4}{3}\pi R^3\). Отношение объемов цилиндра и шара равно \(\frac{V_{\text{цил}}}{V_{\text{шара}}} = \frac{2\pi R^3}{\frac{4}{3}\pi R^3} = \frac{2}{\frac{4}{3}} = 2 \cdot \frac{3}{4} = \frac{6}{4} = \frac{3}{2}\).

В данном случае у нас есть цилиндр, в который вписан шар. Это означает, что шар касается обоих оснований цилиндра и его боковой поверхности.

Первым шагом определим высоту цилиндра. Поскольку шар вписан в цилиндр и касается обоих оснований, высота цилиндра должна быть равна диаметру шара. Если радиус шара обозначим как \(R\), то диаметр шара равен \(2R\). Следовательно, высота цилиндра \(h\) равна \(2R\), то есть \(h = 2R\).

Далее определим радиус основания цилиндра. Поскольку шар вписан в цилиндр и касается его боковой поверхности, радиус основания цилиндра должен быть равен радиусу шара. Если радиус основания цилиндра обозначим как \(R_{\text{цил}}\), то \(R_{\text{цил}} = R\).

Теперь запишем формулу для объема цилиндра. Объем цилиндра вычисляется по формуле \(V_{\text{цил}} = \pi R_{\text{цил}}^2 h\). Подставляя найденные значения радиуса основания и высоты цилиндра в терминах радиуса шара, получаем \(V_{\text{цил}} = \pi (R)^2 (2R) = \pi R^2 \cdot 2R = 2\pi R^3\).

Затем запишем формулу для объема шара. Объем шара с радиусом \(R\) вычисляется по формуле \(V_{\text{шара}} = \frac{4}{3}\pi R^3\).

Нам нужно найти отношение объема цилиндра к объему шара, то есть \(\frac{V_{\text{цил}}}{V_{\text{шара}}}\). Подставим полученные выражения для объемов в это отношение: \(\frac{V_{\text{цил}}}{V_{\text{шара}}} = \frac{2\pi R^3}{\frac{4}{3}\pi R^3}\).

Теперь упростим это выражение. Мы можем сократить \(\pi R^3\) в числителе и знаменателе, так как \(R\) не равен нулю. Получаем \(\frac{2}{\frac{4}{3}}\).

Чтобы разделить на дробь, нужно умножить на обратную дробь. Таким образом, \(\frac{2}{\frac{4}{3}} = 2 \cdot \frac{3}{4}\).

Выполним умножение: \(2 \cdot \frac{3}{4} = \frac{2 \cdot 3}{4} = \frac{6}{4}\).

Наконец, упростим полученную дробь \(\frac{6}{4}\), разделив числитель и знаменатель на их наибольший общий делитель, который равен 2. Получаем \(\frac{6 \div 2}{4 \div 2} = \frac{3}{2}\).

Таким образом, отношение объема цилиндра к объему вписанного в него шара равно \(\frac{3}{2}\).