ГДЗ по Геометрии 11 класс Номер 542 Атанасян — Подробные Ответы

Основанием пирамиды является ромб со стороной \(a\) и острым углом \(\phi\). В пирамиду вписан конус, образующая которого составляет с плоскостью основания угол \(\theta\). Найдите объём конуса.

Радиус основания вписанного конуса \(r\) равен радиусу окружности, вписанной в ромб. Площадь ромба равна \(S = a^2 \sin \phi\). Также площадь ромба равна полупериметру, умноженному на радиус вписанной окружности: \(S = \frac{1}{2} (4a) r = 2ar\). Приравнивая площади, получаем \(a^2 \sin \phi = 2ar\), откуда \(r = \frac{a \sin \phi}{2}\). Высота конуса \(h\) связана с радиусом и углом \(\theta\) соотношением \(h = r \tan \theta\). Подставляя значение \(r\), получаем \(h = \frac{a \sin \phi}{2} \tan \theta\). Объем конуса находится по формуле \(V = \frac{1}{3} \pi r^2 h\). Подставляем значения \(r\) и \(h\): \(V = \frac{1}{3} \pi \left(\frac{a \sin \phi}{2}\right)^2 \left(\frac{a \sin \phi}{2} \tan \theta\right) = \frac{1}{3} \pi \frac{a^2 \sin^2 \phi}{4} \frac{a \sin \phi \tan \theta}{2} = \frac{\pi a^3 \sin^3 \phi \tan \theta}{24}\).
Ответ: \(V = \frac{a^3 \pi}{24} \sin^3 \phi \cdot \tan \theta\).

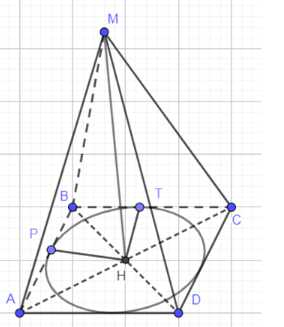
Дано: Конус вписан в пирамиду MABCD. MH — высота конуса и пирамиды. Основание пирамиды ABCD — ромб со стороной AB = \(a\) и углом \(\angle BAD = \phi\). Угол между образующей конуса MP и радиусом основания HP равен \(\angle MPH = \theta\). Найти: Объем конуса V.

Решение:

Первым шагом построим радиусы основания конуса HP перпендикулярно стороне AB и HT перпендикулярно стороне BC ромба. Поскольку MH является высотой пирамиды и конуса, MH перпендикулярно плоскости основания. По теореме о трех перпендикулярах, если HP перпендикулярно AB (проекция MP на плоскость основания), то и сама образующая MP перпендикулярна AB. Аналогично, MT перпендикулярно BC. Отрезки HP и HT являются радиусами окружности, вписанной в ромб, и равны радиусу основания конуса, обозначим его \(r\), то есть \(HP = HT = r\). Отрезки MP и MT являются образующими конуса, обозначим их \(l\), то есть \(MP = MT = l\).

Вторым шагом найдем радиус \(r\) основания конуса. Основание пирамиды — ромб ABCD. Площадь ромба \(S_{ABCD}\) может быть найдена как произведение квадрата стороны на синус угла между сторонами: \(S_{ABCD} = a^2 \sin \phi\). Также площадь ромба равна произведению полупериметра на радиус вписанной окружности. Периметр ромба равен \(4a\), полупериметр равен \(2a\). Следовательно, \(S_{ABCD} = 2a \cdot r\). Приравнивая два выражения для площади ромба, получаем \(a^2 \sin \phi = 2ar\). Из этого уравнения выразим радиус \(r\): \(r = \frac{a^2 \sin \phi}{2a} = \frac{a \sin \phi}{2}\). Таким образом, радиус основания конуса \(HP = r = \frac{a \sin \phi}{2}\).

Третьим шагом найдем высоту конуса MH. Рассмотрим прямоугольный треугольник \(\triangle MHP\). В этом треугольнике MH является катетом, противолежащим углу \(\theta\), а HP является катетом, прилежащим к углу \(\theta\). Тангенс угла \(\theta\) определяется как отношение противолежащего катета к прилежащему: \(\tan \theta = \frac{MH}{HP}\). Отсюда выразим высоту MH: \(MH = HP \tan \theta\). Подставим найденное значение радиуса \(HP = \frac{a \sin \phi}{2}\): \(MH = \frac{a \sin \phi}{2} \tan \theta\). Высота конуса \(h = MH\).

Четвертым шагом вычислим объем конуса. Объем конуса V находится по формуле \(V = \frac{1}{3} \pi r^2 h\). Подставим в эту формулу найденные значения радиуса \(r = \frac{a \sin \phi}{2}\) и высоты \(h = \frac{a \sin \phi}{2} \tan \theta\): \(V = \frac{1}{3} \pi \left(\frac{a \sin \phi}{2}\right)^2 \left(\frac{a \sin \phi}{2} \tan \theta\right)\). Возведем радиус в квадрат: \(r^2 = \left(\frac{a \sin \phi}{2}\right)^2 = \frac{a^2 \sin^2 \phi}{4}\). Теперь подставим это обратно в формулу объема: \(V = \frac{1}{3} \pi \frac{a^2 \sin^2 \phi}{4} \frac{a \sin \phi \tan \theta}{2}\). Перемножим числители и знаменатели: \(V = \frac{\pi \cdot a^2 \sin^2 \phi \cdot a \sin \phi \tan \theta}{3 \cdot 4 \cdot 2} = \frac{\pi a^{2+1} \sin^{2+1} \phi \tan \theta}{24} = \frac{\pi a^3 \sin^3 \phi \tan \theta}{24}\).

Таким образом, объем конуса равен \(V = \frac{a^3 \pi}{24} \sin^3 \phi \cdot \tan \theta\).

Ответ: \(V = \frac{a^3 \pi}{24} \sin^3 \phi \cdot \tan \theta\).