Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 537 Атанасян — Подробные Ответы
В усечённой пирамиде соответственные стороны оснований относятся как 2 : 5. В каком отношении делится её объём плоскостью, проходящей через середину высоты этой пирамиды параллельно основаниям?
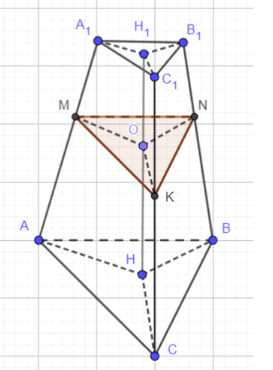
Дано: усечённая пирамида \(ABCA_1B_1C_1\), сечение \(MNK\) проходит через середину высоты \(OH_1 = OH\), \(O \in MNK\), \(\frac{a}{b} = \frac{AC}{A_1C_1} = \frac{5}{2}\). Найти: \(\frac{V_1}{V_2}\).
Решение:
Плоскость \(MNK\) является средним сечением усечённой пирамиды, так как проходит через середину высоты параллельно основаниям.
Сторона среднего сечения \(MK = \frac{AC + A_1C_1}{2}\). Пусть \(AC = a\) и \(A_1C_1 = b\). Тогда \(b = \frac{2}{5}a\).
\(MK = \frac{a + \frac{2}{5}a}{2} = \frac{\frac{7}{5}a}{2} = \frac{7}{10}a\).
Отношение площадей подобных фигур равно квадрату отношения соответствующих сторон.
\(\frac{S_{A_1B_1C_1}}{S_{ABC}} = \left(\frac{A_1C_1}{AC}\right)^2 = \left(\frac{b}{a}\right)^2 = \left(\frac{2}{5}\right)^2 = \frac{4}{25} = 0.16\).
\(\frac{S_{MNK}}{S_{ABC}} = \left(\frac{MK}{AC}\right)^2 = \left(\frac{\frac{7}{10}a}{a}\right)^2 = \left(\frac{7}{10}\right)^2 = \frac{49}{100} = 0.49\).
Объём усечённой пирамиды находится по формуле \(V = \frac{1}{3}h(S_1 + S_2 + \sqrt{S_1 S_2})\).
Сечение \(MNK\) делит усечённую пирамиду на две меньшие усечённые пирамиды с высотой \(h\), равной половине высоты исходной пирамиды.
Объём верхней части \(V_1\) (основания \(A_1B_1C_1\) и \(MNK\)): \(V_1 = \frac{1}{3}h(S_{A_1B_1C_1} + S_{MNK} + \sqrt{S_{A_1B_1C_1} S_{MNK}})\).
Объём нижней части \(V_2\) (основания \(MNK\) и \(ABC\)): \(V_2 = \frac{1}{3}h(S_{MNK} + S_{ABC} + \sqrt{S_{MNK} S_{ABC}})\).
Отношение объёмов:
\(\frac{V_1}{V_2} = \frac{S_{A_1B_1C_1} + S_{MNK} + \sqrt{S_{A_1B_1C_1} S_{MNK}}}{S_{MNK} + S_{ABC} + \sqrt{S_{MNK} S_{ABC}}}\)
Подставим \(S_{A_1B_1C_1} = 0.16 S_{ABC}\) и \(S_{MNK} = 0.49 S_{ABC}\):
\(\frac{V_1}{V_2} = \frac{0.16 S_{ABC} + 0.49 S_{ABC} + \sqrt{0.16 S_{ABC} \cdot 0.49 S_{ABC}}}{0.49 S_{ABC} + S_{ABC} + \sqrt{0.49 S_{ABC} \cdot S_{ABC}}}\)
\(\frac{V_1}{V_2} = \frac{0.16 + 0.49 + \sqrt{0.16 \cdot 0.49}}{0.49 + 1 + \sqrt{0.49 \cdot 1}}\)
\(\frac{V_1}{V_2} = \frac{0.65 + \sqrt{0.0784}}{1.49 + \sqrt{0.49}}\)
\(\frac{V_1}{V_2} = \frac{0.65 + 0.28}{1.49 + 0.7}\)
\(\frac{V_1}{V_2} = \frac{0.93}{2.19} = \frac{93}{219} = \frac{31}{73}\)
Ответ: \(\frac{31}{73}\).
Дано: усечённая пирамида \(ABCA_1B_1C_1\), сечение \(MNK\) проходит через середину высоты \(OH_1 = OH\), \(O \in MNK\), отношение соответствующих сторон оснований \(\frac{AC}{A_1C_1} = \frac{5}{2}\). Найти: отношение объёмов частей, на которые пирамида делится плоскостью \(MNK\), \(\frac{V_1}{V_2}\).
Решение:
Плоскость \(MNK\) проходит через середину высоты усечённой пирамиды и параллельна её основаниям. Это означает, что сечение \(MNK\) является средним сечением усечённой пирамиды. Среднее сечение усечённой пирамиды является многоугольником, подобным основаниям, а его стороны равны полусумме соответствующих сторон оснований.
Пусть \(AC = a\) и \(A_1C_1 = b\). По условию, \(\frac{a}{b} = \frac{5}{2}\), откуда \(b = \frac{2}{5}a\).
Сторона среднего сечения \(MK\) соответствует стороне \(AC\) и \(A_1C_1\). Поскольку \(MNK\) — среднее сечение, \(MK\) является средней линией соответствующей боковой грани или трапеции, образованной высотами и сторонами оснований. Таким образом, \(MK = \frac{AC + A_1C_1}{2}\).
Подставляя значения \(AC = a\) и \(A_1C_1 = \frac{2}{5}a\), получаем \(MK = \frac{a + \frac{2}{5}a}{2} = \frac{\frac{5a + 2a}{5}}{2} = \frac{\frac{7a}{5}}{2} = \frac{7a}{10}\).
Отношение стороны среднего сечения к стороне большего основания равно \(\frac{MK}{AC} = \frac{\frac{7a}{10}}{a} = \frac{7}{10}\).
Отношение стороны меньшего основания к стороне большего основания равно \(\frac{A_1C_1}{AC} = \frac{b}{a} = \frac{2}{5}\).
Площади подобных многоугольников относятся как квадраты их соответствующих сторон.
Отношение площади меньшего основания к площади большего основания: \(\frac{S_{A_1B_1C_1}}{S_{ABC}} = \left(\frac{A_1C_1}{AC}\right)^2 = \left(\frac{2}{5}\right)^2 = \frac{4}{25} = 0.16\).
Отношение площади среднего сечения к площади большего основания: \(\frac{S_{MNK}}{S_{ABC}} = \left(\frac{MK}{AC}\right)^2 = \left(\frac{7}{10}\right)^2 = \frac{49}{100} = 0.49\).
Плоскость \(MNK\) делит исходную усечённую пирамиду на две меньшие усечённые пирамиды. Высота каждой из этих меньших пирамид равна половине высоты исходной усечённой пирамиды. Пусть высота исходной пирамиды равна \(H\), тогда высота каждой из меньших пирамид равна \(h = \frac{H}{2}\).
Объём усечённой пирамиды с высотой \(h\) и площадями оснований \(S_1\) и \(S_2\) вычисляется по формуле \(V = \frac{1}{3}h(S_1 + S_2 + \sqrt{S_1 S_2})\).
Верхняя часть (пирамида с основаниями \(A_1B_1C_1\) и \(MNK\)) имеет объём \(V_1 = \frac{1}{3}h(S_{A_1B_1C_1} + S_{MNK} + \sqrt{S_{A_1B_1C_1} S_{MNK}})\).
Нижняя часть (пирамида с основаниями \(MNK\) и \(ABC\)) имеет объём \(V_2 = \frac{1}{3}h(S_{MNK} + S_{ABC} + \sqrt{S_{MNK} S_{ABC}})\).
Найдём отношение объёмов \(\frac{V_1}{V_2}\):
\(\frac{V_1}{V_2} = \frac{\frac{1}{3}h(S_{A_1B_1C_1} + S_{MNK} + \sqrt{S_{A_1B_1C_1} S_{MNK}})}{\frac{1}{3}h(S_{MNK} + S_{ABC} + \sqrt{S_{MNK} S_{ABC}})}\)
Сокращая \(\frac{1}{3}h\), получаем:
\(\frac{V_1}{V_2} = \frac{S_{A_1B_1C_1} + S_{MNK} + \sqrt{S_{A_1B_1C_1} S_{MNK}}}{S_{MNK} + S_{ABC} + \sqrt{S_{MNK} S_{ABC}}}\)
Выразим площади \(S_{A_1B_1C_1}\) и \(S_{MNK}\) через \(S_{ABC}\): \(S_{A_1B_1C_1} = 0.16 S_{ABC}\) и \(S_{MNK} = 0.49 S_{ABC}\).
\(\frac{V_1}{V_2} = \frac{0.16 S_{ABC} + 0.49 S_{ABC} + \sqrt{0.16 S_{ABC} \cdot 0.49 S_{ABC}}}{0.49 S_{ABC} + S_{ABC} + \sqrt{0.49 S_{ABC} \cdot S_{ABC}}}\)
\(\frac{V_1}{V_2} = \frac{(0.16 + 0.49)S_{ABC} + \sqrt{0.16 \cdot 0.49 \cdot S_{ABC}^2}}{(0.49 + 1)S_{ABC} + \sqrt{0.49 \cdot 1 \cdot S_{ABC}^2}}\)
\(\frac{V_1}{V_2} = \frac{0.65 S_{ABC} + \sqrt{0.0784} S_{ABC}}{1.49 S_{ABC} + \sqrt{0.49} S_{ABC}}\)
\(\frac{V_1}{V_2} = \frac{0.65 S_{ABC} + 0.28 S_{ABC}}{1.49 S_{ABC} + 0.7 S_{ABC}}\)
Вынося \(S_{ABC}\) за скобки в числителе и знаменателе и сокращая его:
\(\frac{V_1}{V_2} = \frac{(0.65 + 0.28) S_{ABC}}{(1.49 + 0.7) S_{ABC}}\)
\(\frac{V_1}{V_2} = \frac{0.93}{2.19}\)
Чтобы избавиться от десятичных дробей, умножим числитель и знаменатель на 100:
\(\frac{V_1}{V_2} = \frac{93}{219}\)
Сократим дробь, найдя наибольший общий делитель. Оба числа делятся на 3.
\(93 \div 3 = 31\)
\(219 \div 3 = 73\)
Таким образом, \(\frac{V_1}{V_2} = \frac{31}{73}\).
Ответ: \(\frac{31}{73}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.