ГДЗ по Геометрии 11 класс Номер 536 Атанасян — Подробные Ответы

Два ребра тетраэдра равны \(b\), а остальные четыре ребра равны \(a\). Найдите объём тетраэдра, если рёбра длины \(b\): а) имеют общие точки; б) не имеют общих точек

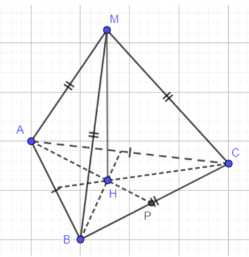
а) Дан тетраэдр \(ABCM\). Ребра \(AC = AB = b\), а ребра \(MA = MC = MB = BC = a\). Требуется найти объем тетраэдра \(V\).

Основанием тетраэдра является треугольник \(ABC\) со сторонами \(AC = AB = b\) и \(BC = a\). Так как \(MA = MC = MB = a\), вершина \(M\) проецируется в центр описанной окружности основания \(\triangle ABC\). Обозначим эту проекцию через \(H\). \(MH\) — высота тетраэдра. \(H\) является центром описанной окружности \(\triangle ABC\).

Найдем высоту \(AP\) в равнобедренном треугольнике \(ABC\), опущенную на основание \(BC\). По теореме Пифагора в \(\triangle APC\): \(AP^2 = AC^2 — CP^2\). Так как \(P\) — середина \(BC\), \(CP = \frac{1}{2} BC = \frac{a}{2}\).
\(AP^2 = b^2 — \left(\frac{a}{2}\right)^2 = b^2 — \frac{a^2}{4}\).
\(AP = \sqrt{b^2 — \frac{a^2}{4}}\).

Площадь основания \(\triangle ABC\) равна \(S_{ABC} = \frac{1}{2} BC \cdot AP = \frac{1}{2} a \sqrt{b^2 — \frac{a^2}{4}}\).

Радиус описанной окружности \(\triangle ABC\) (со сторонами \(a, b, b\)) находится по формуле \(R = \frac{abc}{4S_{ABC}}\), где \(c\) — третья сторона. В данном случае стороны \(a, b, b\).
\(R = \frac{a \cdot b \cdot b}{4 \cdot \frac{1}{2} a \sqrt{b^2 — \frac{a^2}{4}}} = \frac{ab^2}{2a \sqrt{b^2 — \frac{a^2}{4}}} = \frac{b^2}{2 \sqrt{b^2 — \frac{a^2}{4}}} = \frac{b^2}{\sqrt{4b^2 — a^2}}\).
Следовательно, \(AH = R = \frac{b^2}{\sqrt{4b^2 — a^2}}\).

Теперь найдем высоту тетраэдра \(MH\) из прямоугольного треугольника \(\triangle MAH\). По теореме Пифагора: \(MH^2 = MA^2 — AH^2\).
\(MH^2 = a^2 — \left(\frac{b^2}{\sqrt{4b^2 — a^2}}\right)^2 = a^2 — \frac{b^4}{4b^2 — a^2} = \frac{a^2(4b^2 — a^2) — b^4}{4b^2 — a^2} = \frac{4a^2b^2 — a^4 — b^4}{4b^2 — a^2}\).
\(MH = \sqrt{\frac{4a^2b^2 — a^4 — b^4}{4b^2 — a^2}}\).

Объем тетраэдра \(V = \frac{1}{3} S_{ABC} \cdot MH\).
\(V = \frac{1}{3} \left(\frac{1}{2} a \sqrt{b^2 — \frac{a^2}{4}}\right) \left(\sqrt{\frac{4a^2b^2 — a^4 — b^4}{4b^2 — a^2}}\right)\)
\(V = \frac{1}{6} a \sqrt{\frac{4b^2 — a^2}{4}} \sqrt{\frac{4a^2b^2 — a^4 — b^4}{4b^2 — a^2}}\)
\(V = \frac{1}{6} a \frac{\sqrt{4b^2 — a^2}}{2} \frac{\sqrt{4a^2b^2 — a^4 — b^4}}{\sqrt{4b^2 — a^2}}\)
\(V = \frac{a}{12} \sqrt{4a^2b^2 — a^4 — b^4}\).

Ответ: \(V = \frac{a}{12} \sqrt{4a^2b^2 — a^4 — b^4}\).

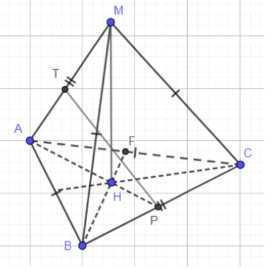
б) Дан тетраэдр \(ABCM\) с ребрами \(MA = BC = b\) и \(AC = MC = MB = AB = a\). Требуется найти объем тетраэдра \(V\).

Основание тетраэдра — равнобедренный треугольник \(ABC\) со сторонами \(AC = AB = a\) и \(BC = b\). Высота \(AP\) в \(\triangle ABC\) на сторону \(BC\) равна \(AP = \sqrt{AC^2 — (\frac{1}{2}BC)^2} = \sqrt{a^2 — \frac{b^2}{4}}\).

Площадь основания \(\triangle ABC\) равна \(S_{ABC} = \frac{1}{2} AP \cdot BC = \frac{1}{2} \sqrt{a^2 — \frac{b^2}{4}} \cdot b = \frac{b}{4} \sqrt{4a^2 — b^2}\).

Треугольник \(MBC\) также равнобедренный со сторонами \(MC = MB = a\) и \(BC = b\). Высота \(MP\) в \(\triangle MBC\) на сторону \(BC\) равна \(MP = \sqrt{MB^2 — (\frac{1}{2}BC)^2} = \sqrt{a^2 — \frac{b^2}{4}}\). Таким образом, \(AP = MP\).

Поскольку \(AP = MP\) и \(M, A\) равноудалены от \(B, C\), плоскость \(MPA\) перпендикулярна \(BC\). Высота тетраэдра \(MH\) лежит в плоскости \(MPA\).

В треугольнике \(MAP\) проведем высоту \(PT\) к стороне \(AM\). Поскольку \(AP = MP\), \(\triangle MAP\) равнобедренный, и \(PT\) также является медианой, поэтому \(AT = TM = \frac{1}{2} AM\). По условию \(MA = b\), следовательно \(AT = \frac{b}{2}\).

В прямоугольном треугольнике \(PTA\) по теореме Пифагора \(PT = \sqrt{AP^2 — AT^2} = \sqrt{\left(\sqrt{a^2 — \frac{b^2}{4}}\right)^2 — \left(\frac{b}{2}\right)^2} = \sqrt{a^2 — \frac{b^2}{4} — \frac{b^2}{4}} =\)
\(= \sqrt{a^2 — \frac{b^2}{2}} = \sqrt{\frac{4a^2 — 2b^2}{4}} = \frac{\sqrt{4a^2 — 2b^2}}{2}\).

Площадь треугольника \(PMA\) может быть выражена двумя способами: \(S_{PMA} = \frac{1}{2} PT \cdot AM\) и \(S_{PMA} = \frac{1}{2} MH \cdot AP\).
\(\frac{1}{2} \cdot \frac{\sqrt{4a^2 — 2b^2}}{2} \cdot b = \frac{1}{2} MH \cdot \sqrt{a^2 — \frac{b^2}{4}}\).
\(\frac{b \sqrt{4a^2 — 2b^2}}{4} = \frac{1}{2} MH \cdot \frac{\sqrt{4a^2 — b^2}}{2}\).
\(\frac{b \sqrt{4a^2 — 2b^2}}{4} = \frac{MH \sqrt{4a^2 — b^2}}{4}\).
Отсюда \(MH = \frac{b \sqrt{4a^2 — 2b^2}}{\sqrt{4a^2 — b^2}}\).

Объем тетраэдра \(V = \frac{1}{3} S_{ABC} \cdot MH\).
\(V = \frac{1}{3} \left(\frac{b}{4} \sqrt{4a^2 — b^2}\right) \left(\frac{b \sqrt{4a^2 — 2b^2}}{\sqrt{4a^2 — b^2}}\right)\).
\(V = \frac{1}{3} \cdot \frac{b}{4} \cdot b \sqrt{4a^2 — 2b^2}\).
\(V = \frac{b^2}{12} \sqrt{4a^2 — 2b^2}\).

Ответ: \(V = \frac{b^2}{12} \sqrt{4a^2 — 2b^2}\).

а) Дан тетраэдр \(ABCM\). По условию \(AC = AB = b\) и \(MA = MC = MB = BC = a\). Требуется найти объем тетраэдра \(V\).

Рассмотрим основание тетраэдра — треугольник \(ABC\). У него стороны \(AC = AB = b\) и \(BC = a\). Это равнобедренный треугольник.

Поскольку \(MA = MC = MB = a\), вершина \(M\) равноудалена от вершин основания \(A, B, C\). Следовательно, проекция вершины \(M\) на плоскость основания \(\triangle ABC\), которую обозначим через \(H\), является центром описанной окружности треугольника \(ABC\). \(MH\) является высотой тетраэдра.

Найдем высоту \(AP\) в равнобедренном треугольнике \(ABC\), опущенную из вершины \(A\) на основание \(BC\). Точка \(P\) является серединой отрезка \(BC\), поэтому \(CP = \frac{BC}{2} = \frac{a}{2}\). В прямоугольном треугольнике \(APC\) по теореме Пифагора имеем \(AP^2 = AC^2 — CP^2\). Подставляя значения, получаем \(AP^2 = b^2 — \left(\frac{a}{2}\right)^2 = b^2 — \frac{a^2}{4}\). Отсюда \(AP = \sqrt{b^2 — \frac{a^2}{4}}\).

Площадь основания тетраэдра \(\triangle ABC\) вычисляется как половина произведения основания \(BC\) на высоту \(AP\): \(S_{ABC} = \frac{1}{2} BC \cdot AP = \frac{1}{2} a \sqrt{b^2 — \frac{a^2}{4}}\).

Теперь найдем радиус \(R\) описанной окружности треугольника \(ABC\). Стороны треугольника равны \(a, b, b\). Площадь \(S_{ABC} = \frac{1}{2} a \sqrt{b^2 — \frac{a^2}{4}}\). Радиус описанной окружности находится по формуле \(R = \frac{abc}{4S_{ABC}}\), где \(a, b, c\) — длины сторон треугольника. В нашем случае стороны равны \(a, b, b\).
\(R = \frac{a \cdot b \cdot b}{4 \cdot \frac{1}{2} a \sqrt{b^2 — \frac{a^2}{4}}} = \frac{ab^2}{2a \sqrt{b^2 — \frac{a^2}{4}}} = \frac{b^2}{2 \sqrt{b^2 — \frac{a^2}{4}}}\).
Упростим знаменатель: \(2 \sqrt{b^2 — \frac{a^2}{4}} = \sqrt{4 \left(b^2 — \frac{a^2}{4}\right)} = \sqrt{4b^2 — a^2}\).
Таким образом, радиус описанной окружности \(R = \frac{b^2}{\sqrt{4b^2 — a^2}}\).
Поскольку \(H\) — центр описанной окружности, \(AH = R = \frac{b^2}{\sqrt{4b^2 — a^2}}\).

Теперь найдем высоту тетраэдра \(MH\). Рассмотрим прямоугольный треугольник \(MAH\). Гипотенуза \(MA = a\), катет \(AH = R = \frac{b^2}{\sqrt{4b^2 — a^2}}\). По теореме Пифагора \(MH^2 = MA^2 — AH^2\).
\(MH^2 = a^2 — \left(\frac{b^2}{\sqrt{4b^2 — a^2}}\right)^2 = a^2 — \frac{b^4}{4b^2 — a^2}\).
Приведем к общему знаменателю: \(MH^2 = \frac{a^2(4b^2 — a^2) — b^4}{4b^2 — a^2} = \frac{4a^2b^2 — a^4 — b^4}{4b^2 — a^2}\).
Высота тетраэдра \(MH = \sqrt{\frac{4a^2b^2 — a^4 — b^4}{4b^2 — a^2}}\).

Объем тетраэдра \(V\) вычисляется по формуле \(V = \frac{1}{3} S_{ABC} \cdot MH\).
Подставим выражения для \(S_{ABC}\) и \(MH\):
\(V = \frac{1}{3} \left(\frac{1}{2} a \sqrt{b^2 — \frac{a^2}{4}}\right) \left(\sqrt{\frac{4a^2b^2 — a^4 — b^4}{4b^2 — a^2}}\right)\).
Упростим выражение под первым корнем: \(\sqrt{b^2 — \frac{a^2}{4}} = \sqrt{\frac{4b^2 — a^2}{4}} = \frac{\sqrt{4b^2 — a^2}}{2}\).
Подставим это обратно в формулу для объема:
\(V = \frac{1}{3} \cdot \frac{1}{2} a \cdot \frac{\sqrt{4b^2 — a^2}}{2} \cdot \sqrt{\frac{4a^2b^2 — a^4 — b^4}{4b^2 — a^2}}\).
\(V = \frac{a}{12} \sqrt{4b^2 — a^2} \cdot \frac{\sqrt{4a^2b^2 — a^4 — b^4}}{\sqrt{4b^2 — a^2}}\).
Сокращая \(\sqrt{4b^2 — a^2}\) (при условии, что \(4b^2 — a^2 > 0\)), получаем:
\(V = \frac{a}{12} \sqrt{4a^2b^2 — a^4 — b^4}\).

Это решение соответствует случаю, когда два ребра длины \(b\) имеют общую точку (например, \(AC\) и \(AB\)).

Ответ: Объем тетраэдра равен \(V = \frac{a}{12} \sqrt{4a^2b^2 — a^4 — b^4}\).

б) Дан тетраэдр \(ABCM\). По условию \(MA = BC = b\) и \(AC = MC = MB = AB = a\). Требуется найти объем тетраэдра \(V\).

Первым шагом рассмотрим основание тетраэдра — треугольник \(ABC\). Поскольку \(AC = AB = a\), треугольник \(ABC\) является равнобедренным. Построим в нем высоту \(AP\) к стороне \(BC\). В равнобедренном треугольнике высота, проведенная к основанию, также является медианой. Следовательно, точка \(P\) — середина отрезка \(BC\), и \(BP = PC = \frac{BC}{2} = \frac{b}{2}\). В прямоугольном треугольнике \(APC\) по теореме Пифагора находим длину высоты \(AP\): \(AP = \sqrt{AC^2 — PC^2} = \sqrt{a^2 — \left(\frac{b}{2}\right)^2} = \sqrt{a^2 — \frac{b^2}{4}}\).

Далее рассмотрим треугольник \(MBC\). По условию \(MC = MB = a\) и \(BC = b\). Этот треугольник также равнобедренный и конгруэнтен треугольнику \(ABC\) по трем сторонам (\(MC=AC=a\), \(MB=AB=a\), \(BC=BC=b\)). Высота \(MP\) в треугольнике \(MBC\) к стороне \(BC\) также является медианой, и ее длина равна \(MP = \sqrt{MB^2 — PC^2} = \sqrt{a^2 — \left(\frac{b}{2}\right)^2} = \sqrt{a^2 — \frac{b^2}{4}}\). Таким образом, \(AP = MP\).

Поскольку \(AP\) и \(MP\) являются высотами в треугольниках \(ABC\) и \(MBC\) соответственно, проведенными к общей стороне \(BC\), и \(AP = MP\), это означает, что плоскость \(MPA\) перпендикулярна ребру \(BC\). Высота тетраэдра \(MH\) от вершины \(M\) до плоскости основания \(ABC\) лежит в плоскости \(MPA\).

Теперь рассмотрим треугольник \(MAP\). У него стороны \(AP = MP = \sqrt{a^2 — \frac{b^2}{4}}\) и \(AM = b\). Этот треугольник равнобедренный. Проведем в нем высоту \(PT\) к стороне \(AM\). Поскольку \(\triangle MAP\) равнобедренный с основанием \(AM\), высота \(PT\) также является медианой, то есть \(T\) — середина \(AM\). Следовательно, \(AT = TM = \frac{AM}{2} = \frac{b}{2}\).

В прямоугольном треугольнике \(PTA\) по теореме Пифагора найдем длину \(PT\): \(PT = \sqrt{AP^2 — AT^2} = \sqrt{\left(\sqrt{a^2 — \frac{b^2}{4}}\right)^2 — \left(\frac{b}{2}\right)^2} = \sqrt{a^2 — \frac{b^2}{4} — \frac{b^2}{4}} =\)
\(= \sqrt{a^2 — \frac{b^2}{2}} = \sqrt{\frac{2a^2 — b^2}{2}} = \frac{\sqrt{4a^2 — 2b^2}}{2}\).

Площадь треугольника \(PMA\) можно вычислить двумя способами: используя основание \(AM\) и высоту \(PT\), или используя основание \(AP\) и высоту \(MH\) (так как \(MH\) — высота тетраэдра, она перпендикулярна плоскости основания \(ABC\), и точка \(H\) лежит на прямой \(AP\), которая является высотой в основании, или более точно, \(H\) — проекция \(M\) на плоскость \(ABC\), и \(H\) лежит на \(AP\) потому что \(AP=MP\)).
\(S_{PMA} = \frac{1}{2} PT \cdot AM\)
\(S_{PMA} = \frac{1}{2} \cdot \frac{\sqrt{4a^2 — 2b^2}}{2} \cdot b = \frac{b \sqrt{4a^2 — 2b^2}}{4}\).
Также \(S_{PMA} = \frac{1}{2} MH \cdot AP\).
Приравниваем выражения для площади:
\(\frac{1}{2} MH \cdot AP = \frac{b \sqrt{4a^2 — 2b^2}}{4}\).
Подставим значение \(AP = \sqrt{a^2 — \frac{b^2}{4}} = \frac{\sqrt{4a^2 — b^2}}{2}\):
\(\frac{1}{2} MH \cdot \frac{\sqrt{4a^2 — b^2}}{2} = \frac{b \sqrt{4a^2 — 2b^2}}{4}\).
\(\frac{MH \sqrt{4a^2 — b^2}}{4} = \frac{b \sqrt{4a^2 — 2b^2}}{4}\).
Отсюда находим высоту тетраэдра \(MH = \frac{b \sqrt{4a^2 — 2b^2}}{\sqrt{4a^2 — b^2}}\).

Наконец, вычислим объем тетраэдра \(V\) по формуле \(V = \frac{1}{3} S_{ABC} \cdot MH\).
Подставим выражения для \(S_{ABC}\) и \(MH\):
\(V = \frac{1}{3} \left(\frac{b}{4} \sqrt{4a^2 — b^2}\right) \left(\frac{b \sqrt{4a^2 — 2b^2}}{\sqrt{4a^2 — b^2}}\right)\).
Сократим \(\sqrt{4a^2 — b^2}\) в числителе и знаменателе:
\(V = \frac{1}{3} \cdot \frac{b}{4} \cdot b \sqrt{4a^2 — 2b^2}\).
\(V = \frac{b^2}{12} \sqrt{4a^2 — 2b^2}\).

Ответ: Объем тетраэдра равен \(V = \frac{b^2}{12} \sqrt{4a^2 — 2b^2}\).