
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 535 Атанасян — Подробные Ответы
Основанием пирамиды является ромб со стороной \(a\). Две боковые грани пирамиды перпендикулярны к плоскости основания и образуют тупой двугранный угол \(\phi\). Две другие боковые грани составляют с плоскостью основания двугранные углы \(\theta\). Найдите объём пирамиды.
В ромбе \(ABCD\) со стороной \(a\) и углом \(\angle ABC = \phi\), площадь основания пирамиды равна \(S_{\text{осн}} = a^2 \sin \phi\).
Высота пирамиды \(MB\) связана с расстоянием от точки \(B\) до сторон ромба и углом \(\theta\). Расстояние от \(B\) до \(AD\) и \(CD\) равно \(BT = PB = a \sin(180^\circ — \phi) = a \sin \phi\).
В прямоугольном треугольнике \(\triangle BMT\), высота \(MB = BT \tan \theta = a \sin \phi \tan \theta\).
Объем пирамиды \(V = \frac{1}{3} S_{\text{осн}} \cdot MB = \frac{1}{3} (a^2 \sin \phi) (a \sin \phi \tan \theta) = \frac{1}{3} a^3 \sin^2 \phi \tan \theta\).
Ответ: \(V = \frac{1}{3} a^3 \sin^2 \phi \tan \theta\).
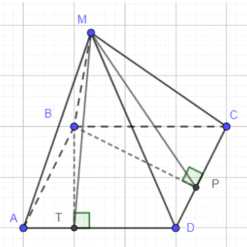
Дано: пирамида \(MABCD\), \(MB\) — высота, основание \(ABCD\) — ромб, \(AB = a\), \(\angle MTB = \theta\), \(\angle MPB = \theta\), \(\angle ABC = \phi\).
Найти: Объем пирамиды \(V\).
Решение:
Угол \(\angle ABC\) является углом ромба. В ромбе сумма смежных углов равна \(180^\circ\), поэтому \(\angle BAD = \angle BCD = 180^\circ — \phi\).
Построим отрезки \(BT\) перпендикулярно \(AD\) и \(BP\) перпендикулярно \(CD\). Поскольку \(MB\) является высотой пирамиды, \(MB\) перпендикулярно плоскости основания \(ABCD\). По теореме о трех перпендикулярах, если проекция \(BT\) (или \(BP\)) перпендикулярна прямой \(AD\) (или \(CD\)) в плоскости основания, то наклонная \(MT\) (или \(MP\)) также перпендикулярна этой прямой. Таким образом, \(MT \perp AD\) и \(MP \perp CD\).
Углы \(\angle MTB\) и \(\angle MPB\) являются линейными углами двугранных углов между боковыми гранями \(MAD\) и \(MCD\) соответственно и плоскостью основания \(ABCD\). По условию, эти углы равны \(\theta\).
Рассмотрим прямоугольные треугольники \(\triangle BMT\) и \(\triangle BPM\). У них общий катет \(BM\) (высота пирамиды). Катеты \(BT\) и \(BP\) являются высотами ромба, опущенными из вершины \(B\) на стороны \(AD\) и \(CD\) соответственно. В ромбе расстояния от вершины до противолежащих сторон равны, а также расстояния от вершины до смежных сторон (в данном случае \(AD\) и \(CD\) являются смежными к углу \(C\), но \(BT\) и \(BP\) are distances to sides \(AD\) and \(CD\)). В ромбе все стороны равны \(a\). Площадь ромба можно найти как произведение стороны на высоту, опущенную на эту сторону, или как \(a^2 \sin(\text{угол})\). Расстояние от вершины \(B\) до стороны \(AD\) (или \(CD\)) в ромбе со стороной \(a\) и углом \(\angle BAD = 180^\circ — \phi\) (или \(\angle BCD = 180^\circ — \phi\)) можно найти как \(a \sin(180^\circ — \phi) = a \sin \phi\). Следовательно, \(BT = PB = a \sin \phi\).
Поскольку \(\triangle BMT\) и \(\triangle BPM\) являются прямоугольными треугольниками с общим катетом \(BM\) и равными катетами \(BT = BP\), эти треугольники равны (\(\triangle BMT \cong \triangle BPM\)).
В прямоугольном треугольнике \(\triangle BMT\) имеем \(\tan \angle MTB = \frac{MB}{BT}\). Подставляя известные значения, получаем \(\tan \theta = \frac{MB}{a \sin \phi}\). Отсюда выражаем высоту \(MB = a \sin \phi \tan \theta\).
Площадь основания пирамиды, ромба \(ABCD\), можно найти по формуле \(S_{\text{осн}} = AD \cdot AB \sin \angle BAD\). Подставляя значения, получаем \(S_{\text{осн}} = a \cdot a \sin(180^\circ — \phi) = a^2 \sin \phi\).
Объем пирамиды находится по формуле \(V = \frac{1}{3} S_{\text{осн}} \cdot MB\). Подставляем найденные значения площади основания и высоты:
\(V = \frac{1}{3} (a^2 \sin \phi) (a \sin \phi \tan \theta) = \frac{1}{3} a^3 \sin^2 \phi \tan \theta\).
Ответ: \(V = \frac{1}{3} a^3 \sin^2 \phi \tan \theta\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!