
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 534 Атанасян — Подробные Ответы
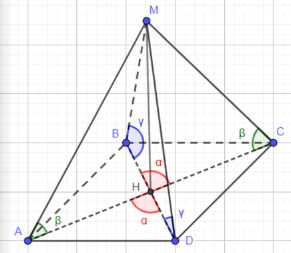
Основанием четырёхугольной пирамиды, высота которой равна \(Н\), является параллелограмм. Диагонали параллелограмма пересекаются под углом \(\alpha\). Попарно равные противоположные боковые рёбра пирамиды образуют с плоскостью основания углы \(\beta\) и \(\gamma\). Найдите объём пирамиды.
Из прямоугольного треугольника, образованного высотой пирамиды, половиной диагонали основания и боковым ребром, получаем, что половина одной диагонали основания равна \(\frac{H}{\text{tg} \gamma}\). Половина другой диагонали основания равна \(\frac{H}{\text{tg} \beta}\). Длины диагоналей основания равны \(AC = \frac{2H}{\text{tg} \beta}\) и \(BD = \frac{2H}{\text{tg} \gamma}\). Площадь основания параллелограмма равна \(S_{\text{осн}} = \frac{1}{2} AC \cdot BD \sin \alpha = \frac{1}{2} \cdot \frac{2H}{\text{tg} \beta} \cdot \frac{2H}{\text{tg} \gamma} \sin \alpha = \frac{2H^2 \sin \alpha}{\text{tg} \beta \text{tg} \gamma}\). Объём пирамиды равен \(V = \frac{1}{3} S_{\text{осн}} H = \frac{1}{3} \cdot \frac{2H^2 \sin \alpha}{\text{tg} \beta \text{tg} \gamma} \cdot H = \frac{2H^3 \sin \alpha}{3 \text{tg} \beta \text{tg} \gamma}\).
Рассмотрим прямоугольный треугольник, образованный высотой пирамиды \(MH\), равной \(h\), и отрезком \(HB\), где \(H\) — проекция вершины \(M\) на плоскость основания. Угол между боковым ребром \(MB\) и плоскостью основания равен \(\gamma\), следовательно, угол \(\angle MBH = \gamma\). В прямоугольном треугольнике \(\Delta MHB\) тангенс угла \(\gamma\) равен отношению противолежащего катета \(MH\) к прилежащему катету \(HB\): \(\text{tg} \gamma = \frac{MH}{HB}\). Подставляя \(MH = h\), получаем \(\text{tg} \gamma = \frac{h}{HB}\). Отсюда выразим \(HB\): \(HB = \frac{h}{\text{tg} \gamma}\).
Аналогично, рассмотрим прямоугольный треугольник, образованный высотой пирамиды \(MH\) и отрезком \(HA\). Угол между боковым ребром \(MA\) и плоскостью основания равен \(\beta\), следовательно, угол \(\angle MAH = \beta\). В прямоугольном треугольнике \(\Delta MAH\) тангенс угла \(\beta\) равен отношению противолежащего катета \(MH\) к прилежащему катету \(HA\): \(\text{tg} \beta = \frac{MH}{HA}\). Подставляя \(MH = h\), получаем \(\text{tg} \beta = \frac{h}{HA}\). Отсюда выразим \(HA\): \(HA = \frac{h}{\text{tg} \beta}\).
Так как основанием пирамиды является параллелограмм, а \(H\) — проекция вершины \(M\) и, как следует из равенства углов прилегающих к диагоналям, является точкой пересечения диагоналей, то \(H\) является серединой диагоналей \(AC\) и \(BD\). Следовательно, \(HA = \frac{1}{2} AC\) и \(HB = \frac{1}{2} BD\).
Из равенства \(HA = \frac{1}{2} AC\) и \(HA = \frac{h}{\text{tg} \beta}\) получаем \(\frac{1}{2} AC = \frac{h}{\text{tg} \beta}\), откуда \(AC = \frac{2h}{\text{tg} \beta}\).
Из равенства \(HB = \frac{1}{2} BD\) и \(HB = \frac{h}{\text{tg} \gamma}\) получаем \(\frac{1}{2} BD = \frac{h}{\text{tg} \gamma}\), откуда \(BD = \frac{2h}{\text{tg} \gamma}\).
Площадь основания параллелограмма \(ABCD\) может быть найдена по формуле площади через диагонали и угол между ними: \(S_{ABCD} = \frac{1}{2} AC \cdot BD \sin \alpha\). Подставим найденные выражения для \(AC\) и \(BD\): \(S_{ABCD} = \frac{1}{2} \cdot \frac{2h}{\text{tg} \beta} \cdot \frac{2h}{\text{tg} \gamma} \sin \alpha\). После упрощения получаем \(S_{ABCD} = \frac{2h^2 \sin \alpha}{\text{tg} \beta \text{tg} \gamma}\).
Объём пирамиды равен одной трети произведения площади основания на высоту: \(V = \frac{1}{3} S_{ABCD} \cdot h\). Подставим выражение для площади основания: \(V = \frac{1}{3} \cdot \frac{2h^2 \sin \alpha}{\text{tg} \beta \text{tg} \gamma} \cdot h\). Окончательно получаем формулу для объёма пирамиды: \(V = \frac{2h^3 \sin \alpha}{3 \text{tg} \beta \text{tg} \gamma}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!