ГДЗ по Геометрии 11 класс Номер 533 Атанасян — Подробные Ответы

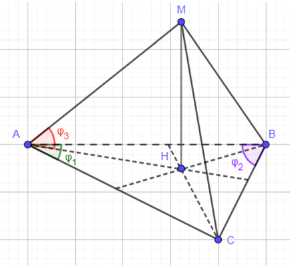
Основанием пирамиды является треугольник, два угла которого равны \(\phi_1\) и \(\phi_2\). Высота пирамиды равна \(h\), а каждое боковое ребро составляет с плоскостью основания угол \(\phi_3\). Найдите объём пирамиды.

Дано: пирамида \(MABC\), \(MH = h\) — высота, \(\angle BAC = \phi_1\), \(\angle ABC = \phi_2\), \(\angle MAH = \angle MBH = \angle MCH = \phi_3\). Найти: \(V\).

Поскольку углы между боковыми ребрами и плоскостью основания равны, проекция вершины \(M\) на плоскость основания \(H\) является центром описанной окружности \(\Delta ABC\). В прямоугольном \(\Delta MHA\), \(AH = MH / \text{tg } \phi_3 = h / \text{tg } \phi_3 = R\), где \(R\) — радиус описанной окружности.

По теореме синусов в \(\Delta ABC\): \(AC = 2R \sin \phi_2 = \frac{2h \sin \phi_2}{\text{tg } \phi_3}\) и \(BC = 2R \sin \phi_1 = \frac{2h \sin \phi_1}{\text{tg } \phi_3}\). Угол между сторонами \(AC\) и \(BC\) равен \(\angle ACB = 180^\circ — (\phi_1 + \phi_2)\), поэтому \(\sin(\angle ACB) = \sin(\phi_1 + \phi_2)\).

Площадь основания: \(S_{\text{осн}} = \frac{1}{2} AC \cdot BC \sin(\phi_1 + \phi_2) = \frac{1}{2} \left(\frac{2h \sin \phi_2}{\text{tg } \phi_3}\right) \left(\frac{2h \sin \phi_1}{\text{tg } \phi_3}\right) \sin(\phi_1 + \phi_2) =\)
\(= \frac{2h^2 \sin \phi_1 \sin \phi_2 \sin(\phi_1 + \phi_2)}{\text{tg}^2 \phi_3}\).

Объем пирамиды: \(V = \frac{1}{3} S_{\text{осн}} h = \frac{1}{3} \left(\frac{2h^2 \sin \phi_1 \sin \phi_2 \sin(\phi_1 + \phi_2)}{\text{tg}^2 \phi_3}\right) h = \frac{2h^3 \sin \phi_1 \sin \phi_2 \sin(\phi_1 + \phi_2)}{3 \text{tg}^2 \phi_3}\).

Дано: пирамида \(MABC\), основание \(\Delta ABC\), \(\angle BAC = \phi_1\), \(\angle ABC = \phi_2\), высота \(MH = h\), \(\angle MAH = \phi_3\). Найти: \(V\).

Решение:

Рассмотрим прямоугольные треугольники \(\Delta MHA\), \(\Delta MHB\) и \(\Delta MHC\). У них общий катет \(MH\). По условию, углы между боковыми ребрами и плоскостью основания равны, то есть \(\angle MAH = \angle MBH = \angle MCH = \phi_3\). Поскольку эти прямоугольные треугольники имеют равные углы при вершине \(M\) и общий катет \(MH\), они равны по катету и острому углу. Из равенства треугольников следует равенство гипотенуз \(AM = BM = MC\) и равенство катетов \(AH = BH = CH\). Точка \(H\) является центром окружности, описанной около треугольника \(ABC\), и \(AH = BH = CH = R\), где \(R\) — радиус описанной окружности.

В прямоугольном треугольнике \(\Delta MHA\) имеем отношение противолежащего катета \(MH\) к прилежащему катету \(AH\), которое равно тангенсу угла \(\phi_3\): \(\frac{MH}{AH} = \text{tg } \phi_3\). Подставляя \(MH = h\), получаем \(\frac{h}{AH} = \text{tg } \phi_3\), откуда находим радиус описанной окружности \(AH = \frac{h}{\text{tg } \phi_3}\).

По теореме синусов в треугольнике \(ABC\), отношение стороны к синусу противолежащего угла равно удвоенному радиусу описанной окружности: \(\frac{AC}{\sin \phi_2} = \frac{BC}{\sin \phi_1} = \frac{AB}{\sin(\angle ACB)} = 2R\). Поскольку сумма углов в треугольнике равна \(180^\circ\), \(\angle ACB = 180^\circ — (\phi_1 + \phi_2)\). Тогда \(\sin(\angle ACB) = \sin(180^\circ — (\phi_1 + \phi_2)) = \sin(\phi_1 + \phi_2)\). Подставляя \(2R = 2AH = \frac{2h}{\text{tg } \phi_3}\), получаем:
\(\frac{AC}{\sin \phi_2} = \frac{2h}{\text{tg } \phi_3}\), откуда \(AC = \frac{2h \cdot \sin \phi_2}{\text{tg } \phi_3}\).
\(\frac{BC}{\sin \phi_1} = \frac{2h}{\text{tg } \phi_3}\), откуда \(BC = \frac{2h \cdot \sin \phi_1}{\text{tg } \phi_3}\).

Найдем площадь основания пирамиды \(S_{\text{осн}} = S_{ABC}\). Площадь треугольника можно найти по формуле \(\frac{1}{2}ab\sin\gamma\), где \(a\) и \(b\) — длины двух сторон, а \(\gamma\) — угол между ними. Используем стороны \(AC\) и \(BC\) и угол \(\angle ACB = \phi_1 + \phi_2\).
\(S_{\text{осн}} = \frac{1}{2} \cdot AC \cdot BC \cdot \sin(\phi_1 + \phi_2)\).
Подставляем найденные выражения для \(AC\) и \(BC\):
\(S_{\text{осн}} = \frac{1}{2} \cdot \left(\frac{2h \cdot \sin \phi_2}{\text{tg } \phi_3}\right) \cdot \left(\frac{2h \cdot \sin \phi_1}{\text{tg } \phi_3}\right) \cdot \sin(\phi_1 + \phi_2)\).
\(S_{\text{осн}} = \frac{1}{2} \cdot \frac{4h^2 \cdot \sin \phi_1 \cdot \sin \phi_2}{\text{tg}^2 \phi_3} \cdot \sin(\phi_1 + \phi_2)\).
\(S_{\text{осн}} = \frac{2h^2 \cdot \sin \phi_1 \cdot \sin \phi_2 \cdot \sin(\phi_1 + \phi_2)}{\text{tg}^2 \phi_3}\).

Найдем объем пирамиды \(V\) по формуле \(V = \frac{1}{3} S_{\text{осн}} \cdot h\).
Подставляем выражение для \(S_{\text{осн}}\):
\(V = \frac{1}{3} \cdot \left(\frac{2h^2 \cdot \sin \phi_1 \cdot \sin \phi_2 \cdot \sin(\phi_1 + \phi_2)}{\text{tg}^2 \phi_3}\right) \cdot h\).
\(V = \frac{2h^3 \cdot \sin \phi_1 \cdot \sin \phi_2 \cdot \sin(\phi_1 + \phi_2)}{3 \cdot \text{tg}^2 \phi_3}\).

Ответ: \(V = \frac{2h^3 \cdot \sin \phi_1 \cdot \sin \phi_2 \cdot \sin(\phi_1 + \phi_2)}{3 \cdot \text{tg}^2 \phi_3}\).