
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 532 Атанасян — Подробные Ответы
В правильной \(n\)-угольной пирамиде плоский угол при вершине равен \(\alpha\), а сторона основания равна \(a\). Найдите объём пирамиды.
Площадь основания: \(S_{\text{осн}} = \frac{na^2}{4 \text{tg} \frac{180^\circ}{n}}\).
Радиус описанной окружности основания: \(R = \frac{a}{2 \text{sin} \frac{180^\circ}{n}}\).
По теореме синусов в боковой грани: \(A_1M = \frac{a}{2 \text{sin} \frac{\alpha}{2}}\).
Высота пирамиды: \(h = \sqrt{A_1M^2 — R^2} = \sqrt{\frac{a^2}{4 \text{sin}^2 \frac{\alpha}{2}} — \frac{a^2}{4 \text{sin}^2 \frac{180^\circ}{n}}} = \frac{a}{2} \sqrt{\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}}\).
Объем пирамиды: \(V = \frac{1}{3} S_{\text{осн}} h = \frac{1}{3} \cdot \frac{na^2}{4 \text{tg} \frac{180^\circ}{n}} \cdot \frac{a}{2} \sqrt{\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}} = \frac{na^3}{24 \text{tg} \frac{180^\circ}{n}} \sqrt{\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}}\).
Ответ: \(V = \frac{na^3}{24 \text{tg} \frac{180^\circ}{n}} \sqrt{\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}}\).
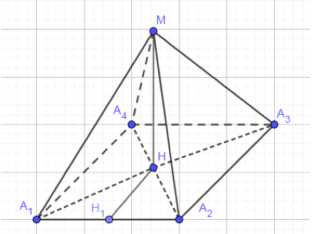
Дана правильная \(n\)-угольная пирамида \(A_1A_2…A_nM\) с основанием \(A_1A_2…A_n\) и вершиной \(M\). Сторона основания равна \(a\), то есть \(A_1A_2 = a\). Высота пирамиды обозначена как \(MH\), где \(H\) — центр основания. Апофема обозначена как \(MH_1\), где \(H_1\) — середина стороны основания. Плоский угол при вершине \(\angle A_1MA_2 = \alpha\). Требуется найти объем пирамиды \(V\).
Первым шагом найдем площадь основания пирамиды. Основанием является правильный \(n\)-угольник со стороной \(a\). Площадь правильного \(n\)-угольника может быть найдена по формуле \(S_{\text{осн}} = \frac{na^2}{4 \text{tg} \frac{180^\circ}{n}}\).
Вторым шагом найдем радиус \(R\) описанной окружности основания. Для правильного \(n\)-угольника со стороной \(a\) радиус описанной окружности равен \(R = \frac{a}{2 \text{sin} \frac{180^\circ}{n}}\). В данной пирамиде \(A_1H\) является радиусом описанной окружности основания, поэтому \(A_1H = R\).
Третьим шагом рассмотрим треугольник \(MA_1A_2\), который является боковой гранью пирамиды. Этот треугольник равнобедренный, так как \(MA_1 = MA_2\) как боковые ребра правильной пирамиды. Угол при вершине \(M\) равен \(\angle A_1MA_2 = \alpha\), а основание \(A_1A_2 = a\). Углы при основании равны \(\angle MA_1A_2 = \angle MA_2A_1 = \frac{180^\circ — \alpha}{2} = 90^\circ — \frac{\alpha}{2}\). Применим теорему синусов к треугольнику \(MA_1A_2\). Отношение стороны к синусу противолежащего угла постоянно: \(\frac{A_1M}{\text{sin}(\angle MA_2A_1)} = \frac{A_1A_2}{\text{sin}(\angle A_1MA_2)}\). Подставляя известные значения, получаем \(\frac{A_1M}{\text{sin}(90^\circ — \frac{\alpha}{2})} = \frac{a}{\text{sin}(\alpha)}\). Отсюда выразим \(A_1M\): \(A_1M = \frac{a \cdot \text{sin}(90^\circ — \frac{\alpha}{2})}{\text{sin}(\alpha)}\). Используя тригонометрическое тождество \(\text{sin}(90^\circ — x) = \text{cos}(x)\), получаем \(A_1M = \frac{a \cdot \text{cos}(\frac{\alpha}{2})}{\text{sin}(\alpha)}\). Далее, используя формулу синуса двойного угла \(\text{sin}(\alpha) = 2 \text{sin}(\frac{\alpha}{2}) \text{cos}(\frac{\alpha}{2})\), упростим выражение для \(A_1M\): \(A_1M = \frac{a \cdot \text{cos}(\frac{\alpha}{2})}{2 \text{sin}(\frac{\alpha}{2}) \text{cos}(\frac{\alpha}{2})} = \frac{a}{2 \text{sin}(\frac{\alpha}{2})}\). Таким образом, длина бокового ребра \(A_1M = \frac{a}{2 \text{sin}(\frac{\alpha}{2})}\).
Четвертым шагом найдем высоту пирамиды \(MH\). Рассмотрим прямоугольный треугольник \(MA_1H\). В этом треугольнике \(MH\) — катет (высота пирамиды \(h\)), \(A_1H\) — другой катет (радиус описанной окружности основания \(R\)), а \(MA_1\) — гипотенуза (боковое ребро). По теореме Пифагора \(MH^2 + A_1H^2 = MA_1^2\), или \(h^2 + R^2 = A_1M^2\). Выразим высоту \(h\): \(h = \sqrt{A_1M^2 — R^2}\). Подставим найденные ранее выражения для \(A_1M\) и \(R\): \(h = \sqrt{\left(\frac{a}{2 \text{sin} \frac{\alpha}{2}}\right)^2 — \left(\frac{a}{2 \text{sin} \frac{180^\circ}{n}}\right)^2} = \sqrt{\frac{a^2}{4 \text{sin}^2 \frac{\alpha}{2}} — \frac{a^2}{4 \text{sin}^2 \frac{180^\circ}{n}}}\). Вынесем общий множитель \(\frac{a^2}{4}\) из-под корня: \(h = \sqrt{\frac{a^2}{4} \left(\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}\right)} = \frac{a}{2} \sqrt{\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}}\).
Пятым шагом найдем объем пирамиды \(V\). Объем пирамиды равен одной трети произведения площади основания на высоту: \(V = \frac{1}{3} S_{\text{осн}} h\). Подставим найденные выражения для \(S_{\text{осн}}\) и \(h\): \(V = \frac{1}{3} \cdot \frac{na^2}{4 \text{tg} \frac{180^\circ}{n}} \cdot \frac{a}{2} \sqrt{\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}}\). Перемножим коэффициенты: \(V = \frac{na^3}{24 \text{tg} \frac{180^\circ}{n}} \sqrt{\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}}\).
Ответ: Объем пирамиды равен \(V = \frac{na^3}{24 \text{tg} \frac{180^\circ}{n}} \sqrt{\frac{1}{\text{sin}^2 \frac{\alpha}{2}} — \frac{1}{\text{sin}^2 \frac{180^\circ}{n}}}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!