ГДЗ по Геометрии 11 класс Номер 530 Атанасян — Подробные Ответы

Боковое ребро правильной четырёхугольной пирамиды составляет с основанием угол \(\phi\), а середина этого ребра удалена от основания пирамиды на расстояние, равное \(m\). Найдите объём пирамиды.

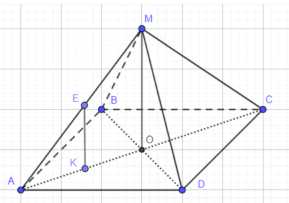
Дано: правильная пирамида ABCDM, \(\angle MAC = \phi\), MO — высота, E — середина AM, EK \(\perp\) плоскости ABCD, EK = m. Найти: V.
Решение. Так как E — середина AM и EK \(\parallel\) MO (оба перпендикулярны основанию), то EK является средней линией треугольника AMO. Следовательно, \(MO = 2 \cdot EK = 2m\). В прямоугольном треугольнике AMO: \(AO = \frac{MO}{tg \phi} = \frac{2m}{tg \phi}\). Диагональ основания \(AC = 2 \cdot AO = \frac{4m}{tg \phi}\). В квадрате ABCD сторона \(a = \frac{AC}{\sqrt{2}} = \frac{4m}{\sqrt{2} tg \phi} = \frac{2\sqrt{2}m}{tg \phi}\). Площадь основания \(S_{осн} = a^2 = \left(\frac{2\sqrt{2}m}{tg \phi}\right)^2 = \frac{8m^2}{tg^2 \phi}\). Объем пирамиды \(V = \frac{1}{3} \cdot S_{осн} \cdot MO = \frac{1}{3} \cdot \frac{8m^2}{tg^2 \phi} \cdot 2m = \frac{16m^3}{3 tg^2 \phi}\).

Ответ: \(V = \frac{16m^3}{3 \cdot tg^2 \phi}\).

Дано: правильная четырёхугольная пирамида ABCDM, где ABCD — квадрат, M — вершина, MO — высота пирамиды, опущенная из вершины M на центр основания O. Угол между боковым ребром AM и основанием ABCD равен \(\phi\), то есть \(\angle MAC = \phi\). Точка E является серединой бокового ребра AM. Отрезок EK перпендикулярен плоскости основания ABCD, причем K лежит на отрезке AO. Длина отрезка EK равна \(m\).
Найти: Объем пирамиды V.

Решение.
Поскольку ABCDM — правильная пирамида, ее основание ABCD является квадратом, а высота MO опущена в центр O основания. Точка O является точкой пересечения диагоналей квадрата AC и BD.
Рассмотрим точку E, которая является серединой отрезка AM. Из точки E опущен перпендикуляр EK на плоскость основания ABCD. Поскольку MO также перпендикулярна плоскости ABCD, отрезки EK и MO параллельны. Точка K лежит на отрезке AO.
В треугольнике AMO, отрезок EK проходит через середину E стороны AM и параллелен стороне MO (так как оба перпендикулярны плоскости основания). Следовательно, по теореме Фалеса или по определению средней линии, EK является средней линией треугольника AMO.
Из свойства средней линии треугольника следует, что длина средней линии равна половине длины стороны, которой она параллельна, и средняя линия соединяет середины двух сторон. Таким образом, EK соединяет середину AM (точка E) с серединой AO (точка K).
Длина EK дана и равна \(m\). Поскольку EK — средняя линия треугольника AMO, параллельная MO, то \(MO = 2 \cdot EK\). Подставляя значение EK, получаем высоту пирамиды \(MO = 2m\).
Теперь рассмотрим прямоугольный треугольник AMO. Угол \(\angle MAO\) равен \(\phi\). В этом прямоугольном треугольнике MO является противолежащим катетом к углу \(\phi\), а AO является прилежащим катетом. Используя определение тангенса угла в прямоугольном треугольнике, имеем \(\tan \phi = \frac{MO}{AO}\).
Из этого соотношения выразим длину отрезка AO: \(AO = \frac{MO}{\tan \phi}\). Подставляя найденное значение MO, получаем \(AO = \frac{2m}{\tan \phi}\).
Отрезок AO является половиной диагонали AC квадрата ABCD, так как O — центр квадрата. Следовательно, длина диагонали \(AC = 2 \cdot AO\). Подставляя значение AO, получаем \(AC = 2 \cdot \frac{2m}{\tan \phi} = \frac{4m}{\tan \phi}\).
В квадрате со стороной \(a\), диагональ связана со стороной соотношением \(AC = a\sqrt{2}\). Используя это соотношение, можем найти длину стороны основания \(a\): \(a = \frac{AC}{\sqrt{2}}\). Подставляя значение AC, получаем \(a = \frac{\frac{4m}{\tan \phi}}{\sqrt{2}} = \frac{4m}{\sqrt{2} \tan \phi}\). Упростим выражение, умножив числитель и знаменатель на \(\sqrt{2}\): \(a = \frac{4m \sqrt{2}}{2 \tan \phi} = \frac{2\sqrt{2}m}{\tan \phi}\).
Площадь основания \(S_{осн}\) правильной четырёхугольной пирамиды равна площади квадрата со стороной \(a\), то есть \(S_{осн} = a^2\). Подставляя найденное значение \(a\), получаем \(S_{осн} = \left(\frac{2\sqrt{2}m}{\tan \phi}\right)^2 = \frac{(2\sqrt{2})^2 m^2}{\tan^2 \phi} = \frac{8m^2}{\tan^2 \phi}\).
Объем пирамиды V вычисляется по формуле \(V = \frac{1}{3} \cdot S_{осн} \cdot h\), где \(h\) — высота пирамиды, которая в данном случае равна MO.
Подставляем найденные значения \(S_{осн}\) и MO в формулу объема: \(V = \frac{1}{3} \cdot \frac{8m^2}{\tan^2 \phi} \cdot 2m\).
Выполняем умножение: \(V = \frac{1 \cdot 8m^2 \cdot 2m}{3 \cdot \tan^2 \phi} = \frac{16m^3}{3 \tan^2 \phi}\).

Ответ: \(V = \frac{16m^3}{3 \cdot \tan^2 \phi}\).