Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 529 Атанасян — Подробные Ответы
Найдите объём правильной треугольной пирамиды, если боковая грань составляет с плоскостью основания угол \(\phi\), а не лежащая в этой грани вершина основания находится на расстоянии \(m\) от неё.
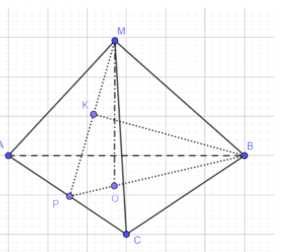
Основание — равносторонний треугольник со стороной \(a\). Высота основания \(BP = \frac{a\sqrt{3}}{2}\). Угол между боковой гранью и основанием \(\phi\). Расстояние от вершины до боковой грани \(m\). В прямоугольном треугольнике, образованном высотой основания, перпендикуляром из вершины к апофеме и отрезком апофемы, \(BP = \frac{m}{\sin \phi}\). Приравнивая выражения для \(BP\), получаем \(\frac{a\sqrt{3}}{2} = \frac{m}{\sin \phi}\), откуда \(a = \frac{2m}{\sqrt{3} \sin \phi}\). Площадь основания \(S_{осн} = \frac{a^2 \sqrt{3}}{4} = \frac{m^2 \sqrt{3}}{3 \sin^2 \phi}\). Радиус вписанной окружности основания \(OP = \frac{a}{2\sqrt{3}} = \frac{m}{3 \sin \phi}\). Высота пирамиды \(h = MO = OP \tan \phi = \frac{m}{3 \sin \phi} \tan \phi = \frac{m}{3 \cos \phi}\). Объем пирамиды \(V = \frac{1}{3} S_{осн} h = \frac{1}{3} \cdot \frac{m^2 \sqrt{3}}{3 \sin^2 \phi} \cdot \frac{m}{3 \cos \phi} = \frac{m^3 \sqrt{3}}{27 \sin^2 \phi \cos \phi}\).
Пусть сторона основания правильной треугольной пирамиды равна \(a\).
Угол между боковой гранью и плоскостью основания равен \(\phi\). Пусть это будет угол между гранью \(MAC\) и основанием \(ABC\). Проведем апофему основания \(OD\) к стороне \(AC\), где \(D\) — середина \(AC\). \(OD\) — радиус вписанной окружности основания, \(OD = r = \frac{a}{2\sqrt{3}}\). Высота пирамиды \(MO\) перпендикулярна основанию. Угол между боковой гранью \(MAC\) и основанием \(ABC\) — это угол между перпендикулярами к общей линии \(AC\) в этих плоскостях, то есть \(\angle MDO = \phi\).
В прямоугольном треугольнике \(MDO\), \(MO = OD \tan \phi = \frac{a}{2\sqrt{3}} \tan \phi\). Высота пирамиды \(h = MO = \frac{a \tan \phi}{2\sqrt{3}}\).
Расстояние от вершины основания, не лежащей в данной боковой грани (пусть это будет вершина \(B\)), до плоскости боковой грани \(MAC\) равно \(m\).
Рассмотрим плоскость, проходящую через вершину \(B\) и перпендикулярную ребру \(AC\). Эта плоскость содержит высоту основания \(BD\) (где \(D\) — середина \(AC\)) и высоту пирамиды \(MO\).
Расстояние от точки \(B\) до плоскости \(MAC\) равно \(m\).
В треугольнике \(MBD\), проведем высоту \(BK\) к \(MD\). Тогда \(BK\) будет перпендикулярно плоскости \(MAC\), и \(BK = m\).
В прямоугольном треугольнике \(BDM\), угол \(\angle MDB = \phi\).
Высота основания \(BD = \frac{a\sqrt{3}}{2}\).
В прямоугольном треугольнике \(BDM\), \(BK\) — высота, опущенная на гипотенузу \(MD\).
Площадь треугольника \(BDM\) может быть выражена как \(\frac{1}{2} BD \cdot MO\) или \(\frac{1}{2} MD \cdot BK\).
\(MD\) — апофема боковой грани. В прямоугольном треугольнике \(MDO\), \(MD = \frac{OD}{\cos \phi} = \frac{a}{2\sqrt{3} \cos \phi}\).
Итак, \(\frac{1}{2} \frac{a\sqrt{3}}{2} \cdot \frac{a \tan \phi}{2\sqrt{3}} = \frac{1}{2} \frac{a}{2\sqrt{3} \cos \phi} \cdot m\).
\(\frac{a^2 \sqrt{3} \sin \phi}{8\sqrt{3} \cos \phi} = \frac{am}{4\sqrt{3} \cos \phi}\).
\(\frac{a^2 \sin \phi}{8} = \frac{am}{4\sqrt{3}}\).
Если \(a \neq 0\), то \(\frac{a \sin \phi}{8} = \frac{m}{4\sqrt{3}}\).
\(a = \frac{8m}{4\sqrt{3} \sin \phi} = \frac{2m}{\sqrt{3} \sin \phi}\).
Теперь найдем высоту пирамиды \(h\):
\(h = \frac{a \tan \phi}{2\sqrt{3}} = \frac{\frac{2m}{\sqrt{3} \sin \phi} \tan \phi}{2\sqrt{3}} = \frac{2m \sin \phi}{\sqrt{3} \sin \phi \cdot 2\sqrt{3} \cos \phi} = \frac{2m}{6 \cos \phi} = \frac{m}{3 \cos \phi}\).
Площадь основания \(S_{осн} = \frac{a^2 \sqrt{3}}{4} = \frac{(\frac{2m}{\sqrt{3} \sin \phi})^2 \sqrt{3}}{4} = \frac{\frac{4m^2}{3 \sin^2 \phi} \sqrt{3}}{4} = \frac{m^2 \sqrt{3}}{3 \sin^2 \phi}\).
Объем пирамиды \(V = \frac{1}{3} S_{осн} h = \frac{1}{3} \cdot \frac{m^2 \sqrt{3}}{3 \sin^2 \phi} \cdot \frac{m}{3 \cos \phi} = \frac{m^3 \sqrt{3}}{27 \sin^2 \phi \cos \phi}\).
Ответ: \(V = \frac{m^3 \sqrt{3}}{27 \sin^2 \phi \cos \phi}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.