ГДЗ по Геометрии 11 класс Номер 527 Атанасян — Подробные Ответы

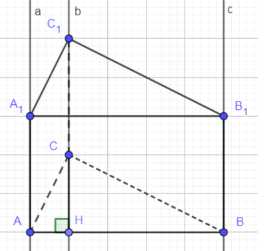
На трёх данных параллельных прямых, не лежащих в одной плоскости, отложены три равных отрезка \(АА_1\), \(ВВ_1\) и \(СС_1\). Докажите, что объём призмы, боковыми рёбрами которой являются эти отрезки, не зависит от положения отрезков на данных прямых.

Длины отрезков \(AA_1\), \(BB_1\), \(CC_1\) постоянны, так как лежат на параллельных прямых. Длины отрезков \(AB\), \(AC\), \(BC\) и \(A_1B_1\), \(A_1C_1\), \(C_1B_1\) постоянны, поскольку прямые \(a\), \(b\), \(c\) параллельны. Высота \(CH\) треугольника \(ABC\) к стороне \(AB\) постоянна, так как стороны треугольника постоянны. Объем призмы выражается формулой \(V = \frac{1}{2} \cdot AB \cdot AA_1 \cdot CH\). Поскольку \(AB\), \(AA_1\) и \(CH\) постоянны, то \(V\) также является постоянной величиной, что и требовалось доказать.

Дано: Призма \(ABCA_1B_1C_1\), боковые рёбра \(AA_1\), \(BB_1\), \(CC_1\) лежат на параллельных прямых \(a\), \(b\), \(c\) соответственно, причем \(a \parallel b \parallel c\), и длины этих рёбер равны \(AA_1 = BB_1 = CC_1\). Доказать: Объём призмы \(V\) является постоянной величиной, то есть \(V = const\).

Доказательство:

Длины отрезков, лежащих на параллельных прямых, не зависят от их конкретного положения на этих прямых, если эти отрезки образованы соответствующими точками оснований призмы, полученными параллельным переносом. Поскольку по условию задачи длины боковых рёбер \(AA_1\), \(BB_1\) и \(CC_1\) равны, и они лежат на параллельных прямых, их длины являются постоянными величинами. Таким образом, \(AA_1 = BB_1 = CC_1 = const\).

Прямые \(a\), \(b\), \(c\) параллельны. Отрезки, соединяющие соответствующие вершины оснований призмы, такие как \(AB\), \(AC\), \(BC\) в нижнем основании и \(A_1B_1\), \(A_1C_1\), \(C_1B_1\) в верхнем основании, имеют постоянные длины. Это связано с тем, что верхнее основание \(A_1B_1C_1\) получается из нижнего основания \(ABC\) параллельным переносом на вектор, равный любому из боковых рёбер. Следовательно, соответствующие стороны оснований равны и их длины постоянны. Таким образом, \(A_1B_1 = AB = A_1C_1 = AC = C_1B_1 = CB = const\).

Построим высоту \(CH\) в основании \(ABC\) из вершины \(C\) к стороне \(AB\). Поскольку, как было показано выше, длины сторон треугольника \(ABC\) (\(AB\), \(AC\), \(BC\)) являются постоянными величинами, то и длина высоты \(CH\), которая определяется сторонами этого треугольника, также является постоянной величиной. Таким образом, \(CH = const\).

Из доказанного в задаче 733 следует формула для объёма данной призмы: \(V = \frac{1}{2} \cdot AB \cdot AA_1 \cdot CH\). Мы установили, что длина стороны основания \(AB\) является постоянной величиной (\(AB = const\)), длина бокового ребра \(AA_1\) является постоянной величиной (\(AA_1 = const\)), и высота основания \(CH\) является постоянной величиной (\(CH = const\)). Подставляя эти постоянные значения в формулу объёма, получаем \(V = \frac{1}{2} \cdot const \cdot const \cdot const\). Произведение постоянных величин всегда является постоянной величиной. Следовательно, объём призмы \(V\) является постоянной величиной, то есть \(V = const\).

Это и требовалось доказать.