ГДЗ по Геометрии 11 класс Номер 526 Атанасян — Подробные Ответы

Докажите, что объём треугольной призмы равен половине произведения площади боковой грани на расстояние от этой грани до параллельного ей ребра.

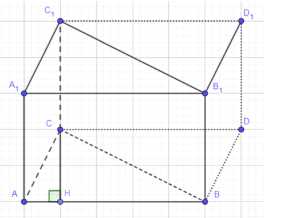
Объем треугольной призмы \(ABCA_1B_1C_1\) можно найти, достроив ее до параллелепипеда \(ABCDA_1B_1C_1D_1\). Объем призмы составляет половину объема этого параллелепипеда, то есть \(V_{призмы} = \frac{1}{2} V_{параллелепипеда}\). Объем параллелепипеда равен произведению площади основания на высоту. Если в качестве основания взять боковую грань \(AA_1BB_1\), то площадь основания будет \(S_{AA_1BB_1}\). Высота параллелепипеда относительно этого основания — это перпендикулярное расстояние от ребра \(CC_1\) до плоскости грани \(AA_1BB_1\). Обозначим это расстояние через \(CH\), где \(CH \perp AA_1BB_1\). Тогда объем параллелепипеда равен \(V_{параллелепипеда} = S_{AA_1BB_1} \cdot CH\). Следовательно, объем треугольной призмы равен \(V_{призмы} = \frac{1}{2} S_{AA_1BB_1} \cdot CH\).

Дано: треугольная призма \(ABCA_1B_1C_1\).
Доказать: объем призмы \(V_{призмы}\) равен половине произведения площади боковой грани \(AA_1BB_1\) на расстояние от этой грани до параллельного ей ребра \(CC_1\).

Решение:
Первым шагом в решении является построение высоты из вершины \(C\) на плоскость боковой грани \(AA_1BB_1\). Пусть \(CH\) — эта высота, где точка \(H\) лежит в плоскости \(AA_1BB_1\) и \(CH \perp AA_1BB_1\). Поскольку ребро \(CC_1\) параллельно плоскости \(AA_1BB_1\), расстояние от ребра \(CC_1\) до плоскости \(AA_1BB_1\) равно длине перпендикуляра, опущенного из любой точки ребра \(CC_1\) на эту плоскость. Таким образом, \(CH\) является этим расстоянием.

Далее, достроим данную треугольную призму \(ABCA_1B_1C_1\) до параллелепипеда \(ABCDA_1B_1C_1D_1\). Это можно сделать, проведя через точку \(C\) прямую, параллельную \(AB\), и через точку \(A\) прямую, параллельную \(BC\), до их пересечения в точке \(D\), так что \(ABCD\) является параллелограммом. Затем построим соответствующие вершины \(D_1\) так, чтобы \(DD_1\) было параллельно и равно \(AA_1\). Полученный параллелепипед \(ABCDA_1B_1C_1D_1\) имеет ту же высоту, что и призма, относительно основания \(ABCD\).

Теперь найдем объем параллелепипеда \(ABCDA_1B_1C_1D_1\). Объем параллелепипеда равен произведению площади основания на высоту. В качестве основания можно взять боковую грань \(AA_1BB_1\). Высота параллелепипеда, соответствующая этому основанию, есть расстояние от любой точки противоположной грани \(DD_1C_1C\) до плоскости \(AA_1BB_1\). Это расстояние равно построенной нами высоте \(CH\). Следовательно, объем параллелепипеда \(V_{параллелепипеда}\) равен площади основания \(AA_1BB_1\) умноженной на высоту \(CH\), то есть \(V_{параллелепипеда} = S_{AA_1BB_1} \cdot CH\).

Треугольная призма \(ABCA_1B_1C_1\) составляет ровно половину объема построенного параллелепипеда \(ABCDA_1B_1C_1D_1\). Это связано с тем, что основание призмы \(ABC\) является треугольником, а основание параллелепипеда \(ABCD\) является параллелограммом, причем площадь треугольника \(ABC\) составляет половину площади параллелограмма \(ABCD\). Призма и параллелепипед имеют одинаковую высоту. Таким образом, объем призмы \(V_{призмы}\) равен половине объема параллелепипеда \(V_{параллелепипеда}\).

Подставляя выражение для объема параллелепипеда, получаем формулу для объема треугольной призмы: \(V_{призмы} = \frac{1}{2} V_{параллелепипеда} = \frac{1}{2} S_{AA_1BB_1} \cdot CH\).

Таким образом, объем треугольной призмы равен половине произведения площади боковой грани на расстояние от этой грани до параллельного ей ребра, что и требовалось доказать.