Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 525 Атанасян — Подробные Ответы
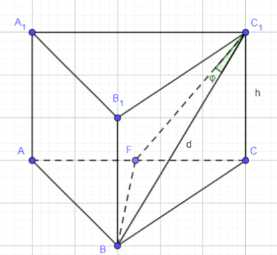
Диагональ боковой грани правильной треугольной призмы равна \(d\) и составляет угол \(\phi\) с плоскостью другой боковой грани. Найдите объём призмы.
АВС — равносторонний треугольник, BF — высота и медиана. \(FC = \frac{1}{2} AC = \frac{1}{2} AB = \frac{1}{2} \frac{2d \sin \phi}{\sqrt{3}} = \frac{d \sin \phi}{\sqrt{3}}\).
В прямоугольном треугольнике \(C_1FC\): \(h = CC_1 = \sqrt{FC_1^2 — FC^2} = \sqrt{(d \cos \phi)^2 — \left(\frac{d \sin \phi}{\sqrt{3}}\right)^2} = \)
\(=\sqrt{d^2 \cos^2 \phi — \frac{d^2 \sin^2 \phi}{3}} = \sqrt{\frac{3d^2 \cos^2 \phi — d^2 \sin^2 \phi}{3}} = d \sqrt{\frac{3 \cos^2 \phi — \sin^2 \phi}{3}}\).
Найдем объем призмы: \(V = S_{осн} \cdot h = \frac{\sqrt{3}}{3} d^2 \sin^2 \phi \cdot d \sqrt{\frac{3 \cos^2 \phi — \sin^2 \phi}{3}} = \frac{\sqrt{3}}{3} d^3 \sin^2 \phi \frac{\sqrt{3 \cos^2 \phi — \sin^2 \phi}}{\sqrt{3}} = \)
\(=\frac{d^3 \sin^2 \phi \sqrt{3 \cos^2 \phi — \sin^2 \phi}}{3}\).
Ответ: \(V = \frac{1}{3} d^3 \sin^2 \phi \sqrt{3 \cos^2 \phi — \sin^2 \phi}\).
Построим отрезок \(BF\) перпендикулярно \(AC\) в основании призмы. Поскольку призма правильная и основание является равносторонним треугольником, \(BF\) является высотой и медианой треугольника \(ABC\). Плоскость боковой грани \(AA_1C_1C\) содержит прямую \(AC\). Так как \(BF \perp AC\), отрезок \(BF\) перпендикулярен плоскости \(AA_1C_1C\). Проекцией отрезка \(BC_1\) на плоскость грани \(AA_1C_1C\) является отрезок \(C_1F\). Угол между диагональю \(BC_1\) и плоскостью грани \(AA_1C_1C\) по определению равен углу между \(BC_1\) и ее проекцией \(C_1F\), то есть \(\angle BC_1F = \phi\).
Рассмотрим прямоугольный треугольник \(BFC_1\). В этом треугольнике катет \(BF\) противолежит углу \(\phi\), а гипотенуза равна \(BC_1 = d\). Следовательно, \(BF = BC_1 \sin \phi = d \sin \phi\). Теперь рассмотрим равносторонний треугольник основания \(ABC\). \(BF\) является высотой этого треугольника. В прямоугольном треугольнике \(ABF\), угол \(\angle BAF = 60^\circ\). Мы имеем соотношение \(BF = AB \sin 60^\circ\). Отсюда находим длину стороны основания \(AB = \frac{BF}{\sin 60^\circ} = \frac{d \sin \phi}{\frac{\sqrt{3}}{2}} = \frac{2d \sin \phi}{\sqrt{3}}\).
Найдем площадь основания призмы \(S_{осн}\). Основание \(ABC\) — равносторонний треугольник со стороной \(AB = \frac{2d \sin \phi}{\sqrt{3}}\). Площадь равностороннего треугольника можно найти по формуле \(S = \frac{\sqrt{3}}{4} a^2\), где \(a\) — длина стороны. Подставляя значение \(AB\), получаем \(S_{осн} = S_{ABC} = \frac{\sqrt{3}}{4} \left(\frac{2d \sin \phi}{\sqrt{3}}\right)^2 = \frac{\sqrt{3}}{4} \frac{4d^2 \sin^2 \phi}{3} = \frac{\sqrt{3} d^2 \sin^2 \phi}{3}\).
Теперь найдем высоту призмы \(h = CC_1\). Рассмотрим прямоугольный треугольник \(C_1FC\). В этом треугольнике гипотенуза \(C_1F\) является проекцией \(BC_1\) на плоскость \(AA_1C_1C\). Из прямоугольного треугольника \(BFC_1\), \(C_1F = BC_1 \cos \phi = d \cos \phi\). Отрезок \(FC\) является медианой в равностороннем треугольнике \(ABC\) от вершины \(C\) к стороне \(AB\), но в данном случае \(F\) — это середина \(AC\), так как \(BF\) — высота и медиана к стороне \(AC\). Следовательно, \(FC = \frac{1}{2} AC\). Поскольку треугольник \(ABC\) равносторонний, \(AC = AB = \frac{2d \sin \phi}{\sqrt{3}}\). Значит, \(FC = \frac{1}{2} \cdot \frac{2d \sin \phi}{\sqrt{3}} = \frac{d \sin \phi}{\sqrt{3}}\). В прямоугольном треугольнике \(C_1FC\) по теореме Пифагора \(CC_1^2 + FC^2 = C_1F^2\). Отсюда \(h^2 = CC_1^2 = C_1F^2 — FC^2 = (d \cos \phi)^2 — \left(\frac{d \sin \phi}{\sqrt{3}}\right)^2 = d^2 \cos^2 \phi — \frac{d^2 \sin^2 \phi}{3} = \)
\(=d^2 \left(\cos^2 \phi — \frac{\sin^2 \phi}{3}\right) = d^2 \left(\frac{3 \cos^2 \phi — \sin^2 \phi}{3}\right)\). Высота призмы равна \(h = \sqrt{d^2 \frac{3 \cos^2 \phi — \sin^2 \phi}{3}} = d \frac{\sqrt{3 \cos^2 \phi — \sin^2 \phi}}{\sqrt{3}}\).
Наконец, найдем объем призмы \(V\). Объем призмы равен произведению площади основания на высоту: \(V = S_{осн} \cdot h\). Подставляя найденные значения, получаем \(V = \left(\frac{\sqrt{3} d^2 \sin^2 \phi}{3}\right) \cdot \left(d \frac{\sqrt{3 \cos^2 \phi — \sin^2 \phi}}{\sqrt{3}}\right) = \frac{\sqrt{3} d^2 \sin^2 \phi \cdot d \sqrt{3 \cos^2 \phi — \sin^2 \phi}}{3 \sqrt{3}} =\)
\(= \frac{d^3 \sin^2 \phi \sqrt{3 \cos^2 \phi — \sin^2 \phi}}{3}\).
Ответ: \(V = \frac{1}{3} d^3 \sin^2 \phi \sqrt{3 \cos^2 \phi — \sin^2 \phi}\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.