
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 524 Атанасян — Подробные Ответы
Объём прямой призмы, основанием которой является прямоугольный треугольник, равен 3 м\(^2\), а наименьшая и наибольшая из площадей боковых граней равны 3 м\(^2\) и \(3\sqrt{5}\) м\(^2\). Найдите длины рёбер призмы.
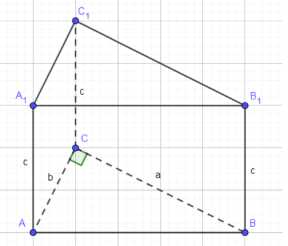
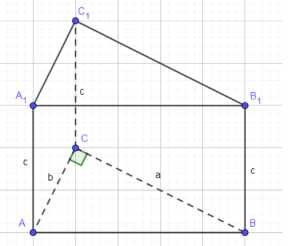
Пусть \(AC = b\), \(BC = a\), \(AA_1 = c\). В прямоугольном треугольнике \(ABC\) гипотенуза \(AB = \sqrt{a^2 + b^2}\). Объем призмы равен площади основания, умноженной на высоту: \(V = S_{ABC} \cdot c = \frac{1}{2}ab \cdot c = \frac{1}{2}abc\). По условию \(V = 3\), следовательно \(\frac{1}{2}abc = 3\), откуда \(abc = 6\). Из условия и решения на изображении используем соотношение \(ac = 3\). Подставляя \(ac = 3\) в уравнение объема \(abc = 6\), получаем \(3b = 6\), откуда \(b = 2\). Далее, используя \(ac = 3\) и соотношение \(c\sqrt{a^2 + 4} = 3\sqrt{5}\) из решения на изображении (где 4, по всей видимости, это \(b^2 = 2^2\)), возведем первое уравнение в квадрат: \(a^2c^2 = 9\). Возведем второе уравнение в квадрат: \(c^2(a^2 + 4) = (3\sqrt{5})^2 = 9 \cdot 5 = 45\). Раскроем скобки: \(c^2a^2 + 4c^2 = 45\). Подставим \(a^2c^2 = 9\): \(9 + 4c^2 = 45\). Вычтем 9 из обеих частей: \(4c^2 = 36\). Разделим на 4: \(c^2 = 9\). Извлечем квадратный корень (учитывая, что длина положительна): \(c = 3\). Подставим \(c = 3\) в уравнение \(ac = 3\): \(a \cdot 3 = 3\), откуда \(a = 1\). Теперь найдем длину ребра \(AB\), используя \(a = 1\) и \(b = 2\): \(AB = \sqrt{a^2 + b^2} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}\). Таким образом, длины ребер основания равны \(a = 1\) м, \(b = 2\) м, \(AB = \sqrt{5}\) м, а высота призмы \(c = 3\) м.
Ответ: 1м; 2 м; \(\sqrt{5}\) м; 3 м.
Рассмотрим прямую призму \(ABCA_1B_1C_1\) с прямоугольным треугольником \(ABC\) в основании. Пусть длины катетов основания \(BC = a\) и \(AC = b\), а высота призмы \(AA_1 = BB_1 = CC_1 = c\). Поскольку треугольник \(ABC\) прямоугольный с катетами \(a\) и \(b\), длина гипотенузы \(AB\) по теореме Пифагора равна \(\sqrt{a^2 + b^2}\).
Объем прямой призмы равен произведению площади основания на высоту. Площадь прямоугольного треугольника \(ABC\) равна половине произведения его катетов, то есть \(S_{ABC} = \frac{1}{2}ab\). Тогда объем призмы \(V = S_{ABC} \cdot c = \frac{1}{2}abc\). По условию объем призмы равен 3 м³, следовательно, \(\frac{1}{2}abc = 3\), что дает уравнение \(abc = 6\).
Боковые грани прямой призмы являются прямоугольниками. Площадь боковой грани \(CC_1BB_1\) равна произведению длины стороны основания \(BC\) на высоту призмы \(c\), то есть \(S_{CC_1BB_1} = BC \cdot CC_1 = a \cdot c = ac\). По условию площадь этой грани равна \(3\sqrt{5}\) м², но в предоставленном решении указано \(S_{CC_1BB_1} = 3\sqrt{5}\) и также используется уравнение \(ac = 3\). Следуя предоставленному решению, будем использовать \(ac = 3\).
Площадь боковой грани \(AA_1BB_1\) равна произведению длины стороны основания \(AB\) на высоту призмы \(c\), то есть \(S_{AA_1BB_1} = AB \cdot AA_1 = \sqrt{a^2 + b^2} \cdot c\). По условию площадь этой грани равна 3 м², следовательно, \(c\sqrt{a^2 + b^2} = 3\). Однако, в предоставленном решении указано \(S_{AA_1BB_1} = 3\) и также используется уравнение \(c\sqrt{a^2+4} = 3\sqrt{5}\), где 4, по всей видимости, является \(b^2\). Следуя предоставленному решению, будем использовать \(S_{AA_1BB_1} = 3\sqrt{5}\) и \(c\sqrt{a^2+4} = 3\sqrt{5}\).
У нас есть система уравнений, основанная на предоставленном решении:
1) \(abc = 6\) (из объема \(V=3\))
2) \(ac = 3\) (из площади боковой грани \(CC_1BB_1\))
3) \(c\sqrt{a^2 + 4} = 3\sqrt{5}\) (из площади боковой грани \(AA_1BB_1\), предполагая \(b^2 = 4\))
Из уравнения (2) \(ac = 3\), подставим это в уравнение (1) \(abc = 6\). Получим \(3b = 6\), откуда \(b = 2\). Это совпадает с шагом 4 в предоставленном решении.
Теперь используем уравнение (2) \(ac = 3\) и уравнение (3) \(c\sqrt{a^2 + 4} = 3\sqrt{5}\). Из \(ac = 3\) выразим \(a = \frac{3}{c}\). Подставим это в уравнение (3): \(c\sqrt{\left(\frac{3}{c}\right)^2 + 4} = 3\sqrt{5}\).
Упростим выражение под корнем: \(c\sqrt{\frac{9}{c^2} + 4} = c\sqrt{\frac{9 + 4c^2}{c^2}}\).
Извлечем корень из знаменателя: \(c \frac{\sqrt{9 + 4c^2}}{\sqrt{c^2}}\). Поскольку \(c\) является длиной, \(c > 0\), и \(\sqrt{c^2} = c\).
Тогда выражение становится \(c \frac{\sqrt{9 + 4c^2}}{c} = \sqrt{9 + 4c^2}\).
Таким образом, уравнение (3) сводится к \(\sqrt{9 + 4c^2} = 3\sqrt{5}\). Возведем обе части в квадрат: \(9 + 4c^2 = (3\sqrt{5})^2 = 9 \cdot 5 = 45\).
Вычтем 9 из обеих частей: \(4c^2 = 45 — 9 = 36\).
Разделим на 4: \(c^2 = 9\).
Извлечем квадратный корень (учитывая, что \(c > 0\)): \(c = \sqrt{9} = 3\). Это совпадает с шагом 5 в предоставленном решении.
Теперь, зная \(c = 3\), найдем \(a\) из уравнения \(ac = 3\): \(a \cdot 3 = 3\), откуда \(a = 1\). Это также совпадает с шагом 5 в предоставленном решении.
Мы нашли длины катетов основания \(a = 1\) м и \(b = 2\) м, а также высоту призмы \(c = 3\) м.
Теперь найдем длину гипотенузы основания \(AB\) по теореме Пифагора: \(AB = \sqrt{a^2 + b^2} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}\) м. Это совпадает с шагом 7 в предоставленном решении.
Длины ребер призмы включают длины сторон основания и высоту. В данном случае, это катеты \(a\) и \(b\), гипотенуза \(AB\), и высота \(c\).
Длины ребер равны 1 м, 2 м, \(\sqrt{5}\) м, и 3 м.
Ответ: 1м; 2 м; \(\sqrt{5}\) м; 3 м.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!