
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 523 Атанасян — Подробные Ответы
В прямой призме, основанием которой является прямоугольный треугольник, пять рёбер равны \(a\), а остальные четыре ребра равны друг другу. Найдите объём призмы.
Рассмотрим прямоугольный треугольник ABC. AB и BC — катеты, AC = \(a\) — гипотенуза. Тогда \(AB^2 = a^2 — AB^2\), что приводит к \(2AB^2 = a^2\), откуда \(AB^2 = \frac{a^2}{2}\). Площадь основания призмы \(S_{осн} = \frac{AB^2}{2} = \frac{a^2/2}{2} = \frac{a^2}{4}\). Объем призмы находится как произведение площади основания на высоту \(AA_1\), которая равна \(a\). Следовательно, \(V = S_{осн} \cdot AA_1 = \frac{a^2}{4} \cdot a = \frac{a^3}{4}\).
Ответ: \(V = \frac{a^3}{4}\).
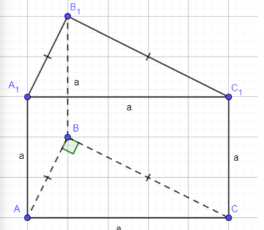
Дано, что у нас есть прямая призма \(ABCA_1B_1C_1\). Основанием призмы является прямоугольный треугольник \(ABC\). Также дано, что катеты \(AB\) и \(BC\) равны, а гипотенуза \(AC\) имеет длину \(a\). Высота призмы \(AA_1\) также равна \(a\). Нам нужно найти объем призмы \(V\).
Первым шагом мы рассматриваем основание призмы, которое является прямоугольным треугольником \(ABC\). Поскольку треугольник \(ABC\) прямоугольный и \(AB = BC\), он является равнобедренным прямоугольным треугольником. По теореме Пифагора для прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. В данном случае \(AC^2 = AB^2 + BC^2\). Подставляя известные значения, получаем \(a^2 = AB^2 + AB^2\), так как \(BC = AB\). Это упрощается до \(a^2 = 2AB^2\). Чтобы найти \(AB^2\), делим обе стороны на 2: \(AB^2 = \frac{a^2}{2}\).
Вторым шагом мы находим площадь основания призмы \(S_{осн}\). Основание — это прямоугольный треугольник с катетами \(AB\) и \(BC\). Площадь прямоугольного треугольника равна половине произведения его катетов: \(S_{осн} = \frac{1}{2} \cdot AB \cdot BC\). Поскольку \(AB = BC\), формула становится \(S_{осн} = \frac{1}{2} \cdot AB^2\). Мы уже нашли, что \(AB^2 = \frac{a^2}{2}\), поэтому подставляем это значение в формулу для площади: \(S_{осн} = \frac{1}{2} \cdot \frac{a^2}{2} = \frac{a^2}{4}\).
Третьим шагом мы находим объем призмы \(V\). Объем прямой призмы равен произведению площади основания на высоту. Высота призмы дана как \(AA_1 = a\). Формула объема призмы: \(V = S_{осн} \cdot AA_1\). Подставляем найденную площадь основания и данную высоту: \(V = \frac{a^2}{4} \cdot a\). Умножая, получаем \(V = \frac{a^3}{4}\).
Таким образом, объем призмы равен \(V = \frac{a^3}{4}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!