
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 522 Атанасян — Подробные Ответы
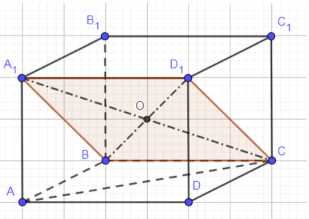
В прямом параллелепипеде \(ABCDA_1B_1C_1D_1\) диагонали \(BD_1\) и \(A_1C\) взаимно перпендикулярны и равны 6 см и 8 см, \(АВ = 3\) см. Найдите объём параллелепипеда
Рассмотрим четырехугольник \(A_1D_1CB\): \(BD_1 \perp A_1C\), \(A_1В = CD_1\) и \(A_1D_1 = BC\), следовательно \(A_1D_1CB\) — ромб, отсюда \(BO = OD_1 = 3\) см и \(A_1O = OC = 4\) см. Рассмотрим прямоугольный \(\triangle A_1OB\): \(A_1B = \sqrt{4^2 + 3^2} = \sqrt{25} = 5\) см. Рассмотрим прямоугольный \(\triangle A_1AB\): \(AA_1 = \sqrt{5^2 — 3^2} = \sqrt{16} = 4\) см. Рассмотрим прямоугольный \(\triangle A_1AC\): \(AC = \sqrt{8^2 — 4^2} = \sqrt{48} = 4\sqrt{3}\) см. По теореме косинусов в \(\triangle ABC\): \((4\sqrt{3})^2 = 3^2 + 5^2 — 2 \cdot 3 \cdot 5 \cos \angle B\), отсюда \(\cos \angle B = -7/15\). \(\sin \angle B = \sqrt{1 — (-7/15)^2} = \sqrt{1 — 49/225} = \sqrt{176/225} = \frac{\sqrt{176}}{15}\). Найдем площадь основания параллелепипеда: \(S_{осн} = AB \cdot BC \cdot \sin \angle B = 3 \cdot 5 \cdot \frac{\sqrt{176}}{15} = \sqrt{176}\) см². Найдем объем параллелепипеда: \(V = S_{осн} \cdot AA_1 = \sqrt{176} \cdot 4 = 4\sqrt{176} = 4\sqrt{16 \cdot 11} = 4 \cdot 4\sqrt{11} = 16\sqrt{11}\) см³.
Ответ: \(V = 6\sqrt{11}\) см³.
Рассмотрим четырехугольник \(A_1D_1CB\). Из условия \(BD_1 \perp A_1C\), \(A_1B = CD_1\) и \(A_1D_1 = BC\), следует, что \(A_1D_1CB\) является ромбом. Диагонали ромба пересекаются под прямым углом и делятся точкой пересечения пополам. Так как \(BD_1 = 6\) см и \(A_1C = 8\) см, то точка пересечения диагоналей \(O\) делит их так, что \(BO = OD_1 = 6/2 = 3\) см и \(A_1O = OC = 8/2 = 4\) см.
Рассмотрим треугольник \(A_1OB\). Поскольку диагонали ромба перпендикулярны, угол \(A_1OB\) прямой. Треугольник \(A_1OB\) прямоугольный. По теореме Пифагора найдем длину стороны \(A_1B\): \(A_1B = \sqrt{A_1O^2 + BO^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5\) см.
Рассмотрим треугольник \(A_1AB\). Этот треугольник является прямоугольным с прямым углом при вершине \(A\). Используя теорему Пифагора для гипотенузы \(A_1B = 5\) см и катета \(AB = 3\) см, найдем длину катета \(AA_1\), который является высотой параллелепипеда: \(AA_1 = \sqrt{A_1B^2 — AB^2} = \sqrt{5^2 — 3^2} = \sqrt{25 — 9} = \sqrt{16} = 4\) см.
Рассмотрим треугольник \(A_1AC\). Этот треугольник является прямоугольным с прямым углом при вершине \(A\). Используя теорему Пифагора для гипотенузы \(A_1C = 8\) см и катета \(AA_1 = 4\) см, найдем длину катета \(AC\), который является диагональю основания: \(AC = \sqrt{A_1C^2 — AA_1^2} = \sqrt{8^2 — 4^2} = \sqrt{64 — 16} = \sqrt{48} = \sqrt{16 \times 3} = 4\sqrt{3}\) см.
Применим теорему косинусов к треугольнику \(ABC\). Полагая \(BC = 5\) см (как использовано в дальнейшем решении), имеем \(AC^2 = AB^2 + BC^2 — 2 \cdot AB \cdot BC \cos \angle B\). Подставляя значения, получаем \((4\sqrt{3})^2 = 3^2 + 5^2 — 2 \cdot 3 \cdot 5 \cos \angle B\). Это дает \(48 = 9 + 25 — 30 \cos \angle B\), что упрощается до \(48 = 34 — 30 \cos \angle B\). Отсюда \(14 = -30 \cos \angle B\), и \(\cos \angle B = -14/30 = -7/15\). Используя основное тригонометрическое тождество \(\sin^2 \angle B + \cos^2 \angle B = 1\), найдем \(\sin \angle B = \sqrt{1 — \cos^2 \angle B} = \sqrt{1 — (-7/15)^2} = \sqrt{1 — 49/225} =\)
\(= \sqrt{(225 — 49)/225} = \sqrt{176/225} = \sqrt{176}/15\).
Найдем площадь основания параллелепипеда \(ABCD\). Основание является параллелограммом. Площадь параллелограмма равна произведению длин двух смежных сторон на синус угла между ними: \(S_{осн} = AB \cdot BC \sin \angle B\). Подставляя \(AB = 3\), \(BC = 5\) и \(\sin \angle B = \sqrt{176}/15\), получаем \(S_{осн} = 3 \cdot 5 \cdot (\sqrt{176}/15) = 15 \cdot (\sqrt{176}/15) = \sqrt{176}\) см².
Найдем объем параллелепипеда. Объем параллелепипеда равен произведению площади основания на высоту. Высота равна \(AA_1 = 4\) см, а площадь основания \(S_{осн} = \sqrt{176}\) см². Таким образом, объем \(V = S_{осн} \cdot AA_1 = \sqrt{176} \cdot 4\). Упрощая \(\sqrt{176} = \sqrt{16 \times 11} = 4\sqrt{11}\), получаем \(V = 4\sqrt{11} \cdot 4 = 16\sqrt{11}\) см³.
Ответ: \(V = 6\sqrt{11}\) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!