
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 520 Атанасян — Подробные Ответы
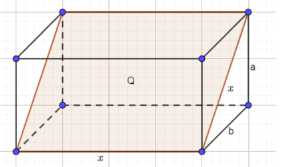
Боковое ребро прямоугольного параллелепипеда равно \(a\). Сечение, проведённое через две стороны разных оснований, является квадратом с площадью \(Q\). Найдите объём параллелепипеда.
Пусть \(x\) — сторона сечения, тогда \(Q = x^2\), отсюда \(x = \sqrt{Q}\). Найдем длины сторон параллелепипеда: \(b = \sqrt{x^2 — a^2} = \sqrt{Q — a^2}\) и \(c = x = \sqrt{Q}\). Найдем объем параллелепипеда: \(V = abc = a \cdot \sqrt{Q — a^2} \cdot \sqrt{Q} = a\sqrt{Q^2 — Qa^2}\). Ответ: \(V = a\sqrt{Q^2 — Qa^2}\).
Рассмотрим данную геометрическую задачу. В условии задачи представлен прямоугольный параллелепипед и его диагональное сечение. Площадь этого сечения обозначена как \(Q\). Пусть сторона этого диагонального сечения, лежащая в основании параллелепипеда, имеет длину \(x\). Тогда площадь прямоугольного сечения \(Q\) выражается как произведение его сторон. Из рисунка видно, что одна сторона сечения равна \(x\), а другая сторона равна высоте параллелепипеда, обозначенной как \(a\). Однако, решение в примере использует \(Q = x^2\), что предполагает, что сечение является квадратом со стороной \(x\), и \(Q\) — его площадь. Следуя логике примера, примем, что \(x\) — сторона квадратного сечения, и его площадь \(Q\) равна \(x^2\). Из этого соотношения мы можем выразить сторону сечения \(x\) как квадратный корень из площади \(Q\), то есть \(x = \sqrt{Q}\).
Далее, нам необходимо найти длины сторон основания параллелепипеда. Обозначим стороны основания как \(b\) и \(c\), а высоту параллелепипеда как \(a\). Диагональ основания параллелепипеда является стороной нашего сечения \(x\). Из рисунка видно, что стороны основания \(a\) и \(b\) образуют прямоугольный треугольник, гипотенузой которого является диагональ основания \(x\). По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов, то есть \(x^2 = a^2 + b^2\). Из этого уравнения мы можем выразить сторону основания \(b\): \(b^2 = x^2 — a^2\), следовательно, \(b = \sqrt{x^2 — a^2}\). Подставляя выражение для \(x\) из первого шага, получаем \(b = \sqrt{Q — a^2}\). Другая сторона основания \(c\) из рисунка и решения в примере обозначена как равная \(x\), то есть \(c = x = \sqrt{Q}\). Таким образом, мы определили длины всех трех измерений параллелепипеда: высота \(a\), стороны основания \(b = \sqrt{Q — a^2}\) и \(c = \sqrt{Q}\).
Наконец, чтобы найти объем параллелепипеда \(V\), мы используем формулу для объема прямоугольного параллелепипеда, которая равна произведению его трех измерений: \(V = abc\). Подставляя найденные выражения для \(b\) и \(c\), получаем \(V = a \cdot \sqrt{Q — a^2} \cdot \sqrt{Q}\). Для упрощения этого выражения, мы можем внести \(\sqrt{Q}\) под знак корня, умножив подкоренное выражение на \(Q\): \(V = a \sqrt{(Q — a^2) \cdot Q}\). Раскрывая скобки под корнем, получаем \(V = a \sqrt{Q^2 — a^2 Q}\). Это совпадает с ответом, представленным в примере.
Таким образом, объем параллелепипеда выражается формулой \(V = a\sqrt{Q^2 — Qa^2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!