
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 519 Атанасян — Подробные Ответы
В прямоугольном параллелепипеде диагонали трёх граней, выходящие из одной вершины, равны 7 см, 8 см и 9 см. Найдите объём параллелепипеда.
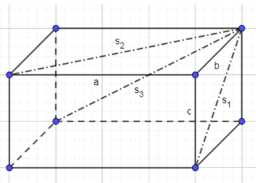
Пусть длины сторон параллелепипеда равны \(a\), \(b\) и \(c\). Диагонали граней, выходящие из одной вершины, равны \(s_1\), \(s_2\) и \(s_3\). Согласно теореме Пифагора, имеем систему уравнений: \(a^2 + c^2 = s_2^2\), \(c^2 + b^2 = s_1^2\), \(a^2 + b^2 = s_3^2\). Используя значения из примера, \(s_1 = 7\), \(s_2 = 8\), \(s_3 = 9\), и порядок уравнений из примера: \(a^2 + c^2 = 81\), \(c^2 + b^2 = 49\), \(a^2 + b^2 = 64\). Вычитая второе уравнение из первого, получаем \(a^2 — b^2 = 32\). Вычитая третье уравнение из первого, получаем \(c^2 — b^2 = 17\). Решая систему уравнений \(c^2 — b^2 = 17\) и \(c^2 + b^2 = 49\), складываем их: \(2c^2 = 66\), откуда \(c^2 = 33\), \(c = \sqrt{33}\). Подставляя \(c^2 = 33\) в \(c^2 + b^2 = 49\), находим \(33 + b^2 = 49\), \(b^2 = 16\), \(b = 4\). Подставляя \(c^2 = 33\) в \(a^2 + c^2 = 81\), находим \(a^2 + 33 = 81\), \(a^2 = 48\), \(a = \sqrt{48} = 4\sqrt{3}\). Объем параллелепипеда равен \(V = abc = (4\sqrt{3}) \cdot 4 \cdot \sqrt{33} = 16 \sqrt{3 \cdot 33} = 16 \sqrt{99} = 16 \cdot 3\sqrt{11} = 48\sqrt{11}\). Ответ: \(V = 48\sqrt{11}\) см³.
Обозначим длины сторон прямоугольного параллелепипеда как \(a\), \(b\) и \(c\). Диагонали трех граней, выходящие из одной вершины, связаны со сторонами по теореме Пифагора. Если диагонали равны \(s_1\), \(s_2\) и \(s_3\), то квадраты этих диагоналей равны суммам квадратов сторон соответствующих граней. Согласно условию задачи и примеру, у нас даны диагонали \(s_1 = 7\) см, \(s_2 = 8\) см и \(s_3 = 9\) см. Мы можем составить следующую систему уравнений, связывающую квадраты сторон и квадраты диагоналей: \(a^2 + c^2 = 9^2 = 81\), \(c^2 + b^2 = 7^2 = 49\), \(a^2 + b^2 = 8^2 = 64\).
Запишем полученную систему уравнений: первое уравнение \(a^2 + c^2 = 81\), второе уравнение \(c^2 + b^2 = 49\), третье уравнение \(a^2 + b^2 = 64\). Наша задача — найти значения \(a\), \(b\) и \(c\) из этой системы.
Вычтем второе уравнение из первого: \((a^2 + c^2) — (c^2 + b^2) = 81 — 49\), что дает \(a^2 — b^2 = 32\).
Вычтем третье уравнение из первого: \((a^2 + c^2) — (a^2 + b^2) = 81 — 64\), что дает \(c^2 — b^2 = 17\).
Теперь у нас есть два новых уравнения: \(a^2 — b^2 = 32\) и \(c^2 — b^2 = 17\). Также у нас осталось одно из исходных уравнений, например, \(c^2 + b^2 = 49\). Рассмотрим систему из уравнений \(c^2 — b^2 = 17\) и \(c^2 + b^2 = 49\). Сложим эти два уравнения: \((c^2 — b^2) + (c^2 + b^2) = 17 + 49\), что дает \(2c^2 = 66\).
Из уравнения \(2c^2 = 66\) находим \(c^2 = \frac{66}{2} = 33\). Следовательно, длина стороны \(c\) равна \(\sqrt{33}\).
Подставим найденное значение \(c^2 = 33\) во второе исходное уравнение \(c^2 + b^2 = 49\): \(33 + b^2 = 49\). Вычтем 33 из обеих частей уравнения: \(b^2 = 49 — 33 = 16\). Следовательно, длина стороны \(b\) равна \(\sqrt{16} = 4\).
Подставим найденное значение \(c^2 = 33\) в первое исходное уравнение \(a^2 + c^2 = 81\): \(a^2 + 33 = 81\). Вычтем 33 из обеих частей уравнения: \(a^2 = 81 — 33 = 48\). Следовательно, длина стороны \(a\) равна \(\sqrt{48}\). Упростим \(\sqrt{48}\): \(\sqrt{48} = \sqrt{16 \cdot 3} = \sqrt{16} \cdot \sqrt{3} = 4\sqrt{3}\). Таким образом, \(a = 4\sqrt{3}\).
Мы нашли длины всех сторон параллелепипеда: \(a = 4\sqrt{3}\) см, \(b = 4\) см, \(c = \sqrt{33}\) см. Теперь найдем объем прямоугольного параллелепипеда по формуле \(V = abc\).
Подставим найденные значения сторон в формулу объема: \(V = (4\sqrt{3}) \cdot 4 \cdot \sqrt{33}\). Перемножим числовые множители и корни: \(V = (4 \cdot 4) \cdot (\sqrt{3} \cdot \sqrt{33}) = 16 \cdot \sqrt{3 \cdot 33}\).
Вычислим произведение под корнем: \(3 \cdot 33 = 99\). Таким образом, \(V = 16 \cdot \sqrt{99}\).
Упростим \(\sqrt{99}\): \(\sqrt{99} = \sqrt{9 \cdot 11} = \sqrt{9} \cdot \sqrt{11} = 3\sqrt{11}\).
Подставим упрощенное значение корня обратно в выражение для объема: \(V = 16 \cdot 3\sqrt{11}\). Перемножим числовые множители: \(16 \cdot 3 = 48\).
Окончательный объем параллелепипеда равен \(V = 48\sqrt{11}\) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!