
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 518 Атанасян — Подробные Ответы
Площади трёх попарно смежных граней прямоугольного параллелепипеда равны \(S_1\), \(S_2\), \(S_3\). Выразите объём этого параллелепипеда через \(S_1\), \(S_2\), \(S_3\) и вычислите его при \(S_1 = 6\) дм\(^2\), \(S_2 = 12\) дм\(^2\), \(S_3 = 18\) дм\(^2\).
Дано: \(S_1 = 6\), \(S_2 = 12\), \(S_3 = 18\). Объём параллелепипеда находится по формуле \(V = \sqrt{S_1 S_2 S_3}\). Подставляя значения, получаем \(V = \sqrt{6 \cdot 12 \cdot 18} = \sqrt{1296} = 36\). Ответ: \(V = 36\) дм³.
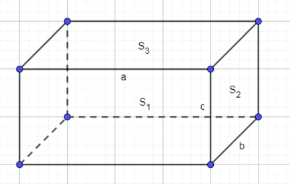
Дано: площади трех граней прямоугольного параллелепипеда равны \(S_1 = 6\) дм², \(S_2 = 12\) дм², \(S_3 = 18\) дм². Пусть измерения параллелепипеда будут \(a\), \(b\), и \(c\). Площади боковых поверхностей (граней) прямоугольного параллелепипеда выражаются как произведение двух его измерений. Мы можем сопоставить данные площади с произведениями сторон: \(S_1 = ac\), \(S_2 = cb\), \(S_3 = ab\).
Объём прямоугольного параллелепипеда вычисляется как произведение его измерений: \(V = a \cdot b \cdot c\).
Рассмотрим произведение данных площадей: \(S_1 \cdot S_2 \cdot S_3 = (ac) \cdot (cb) \cdot (ab)\). Перегруппируем множители: \(S_1 \cdot S_2 \cdot S_3 = a \cdot c \cdot c \cdot b \cdot a \cdot b = a^2 b^2 c^2\).
Заметим, что \(a^2 b^2 c^2 = (abc)^2\). Поскольку \(V = abc\), то \(V^2 = (abc)^2\). Следовательно, мы получили соотношение \(S_1 \cdot S_2 \cdot S_3 = V^2\).
Чтобы найти объём \(V\), нужно извлечь квадратный корень из произведения площадей: \(V = \sqrt{S_1 \cdot S_2 \cdot S_3}\).
Теперь подставим числовые значения площадей, данные в условии задачи: \(V = \sqrt{6 \cdot 12 \cdot 18}\).
Выполним умножение под корнем: \(6 \cdot 12 = 72\), затем \(72 \cdot 18\). \(72 \cdot 18 = 72 \cdot (20 — 2) = 72 \cdot 20 — 72 \cdot 2 = 1440 — 144 = 1296\).
Таким образом, под корнем получаем 1296. Объём равен \(V = \sqrt{1296}\).
Найдем квадратный корень из 1296. Известно, что \(30^2 = 900\) и \(40^2 = 1600\), так что корень находится между 30 и 40. Число 1296 оканчивается на 6, что возможно при возведении в квадрат чисел, оканчивающихся на 4 или 6. Проверим 36: \(36 \cdot 36 = (30 + 6) \cdot (30 + 6) = 30 \cdot 30 + 30 \cdot 6 + 6 \cdot 30 + 6 \cdot 6 = 900 + 180 + \)
\(+180 + 36 = 900 + 360 + 36 = 1260 + 36 = 1296\).
Следовательно, \(V = 36\).
Объём параллелепипеда равен 36 дм³. Ответ: \(V = 36\) дм³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!