ГДЗ по Геометрии 11 класс Номер 517 Атанасян — Подробные Ответы

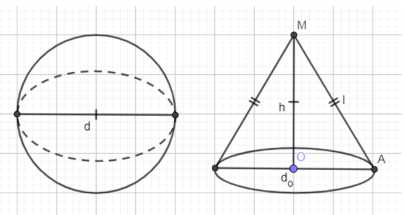
Докажите, что площадь сферы равна площади полной поверхности конуса, высота которого равна диаметру сферы, а диаметр основания равен образующей конуса.

Рассмотрим треугольник MOA: \(\cos \angle A = \frac{OA}{MA} = \frac{d_0/2}{l}\). Так как \(d_0 = l\), то \(\cos \angle A = \frac{l/2}{l} = \frac{1}{2}\), откуда \(\angle A = 60^\circ\). Радиус основания конуса \(OA = r = h \cdot \tan(90^\circ — 60^\circ) = h \cdot \tan 30^\circ = \frac{h}{\sqrt{3}}\).
Площадь основания конуса: \(S_{\text{осн}} = \pi r^2 = \pi \left(\frac{h}{\sqrt{3}}\right)^2 = \frac{\pi h^2}{3}\).
Образующая конуса: \(l = d_0 = 2r = 2 \cdot \frac{h}{\sqrt{3}} = \frac{2h}{\sqrt{3}}\).
Площадь боковой поверхности конуса: \(S_{\text{бок}} = \pi r l = \pi \cdot \frac{h}{\sqrt{3}} \cdot \frac{2h}{\sqrt{3}} = \frac{2\pi h^2}{3}\).
Полная площадь поверхности конуса: \(S_{\text{конуса}} = S_{\text{осн}} + S_{\text{бок}} = \frac{\pi h^2}{3} + \frac{2\pi h^2}{3} = \frac{3\pi h^2}{3} = \pi h^2\).
Площадь сферы: \(S_{\text{сферы}} = 4 \pi R^2\). Так как \(d = h\), радиус сферы \(R = \frac{d}{2} = \frac{h}{2}\). Следовательно, \(S_{\text{сферы}} = 4 \pi \left(\frac{h}{2}\right)^2 = 4 \pi \frac{h^2}{4} = \pi h^2\).
Поскольку \(S_{\text{конуса}} = \pi h^2\) и \(S_{\text{сферы}} = \pi h^2\), то \(S_{\text{конуса}} = S_{\text{сферы}}\), что и требовалось доказать.

Рассмотрим треугольник MOA, где M — вершина конуса, O — центр основания, A — точка на окружности основания. MO — высота конуса \(h\), OA — радиус основания конуса \(r\), MA — образующая конуса \(l\). В прямоугольном треугольнике MOA косинус угла A равен отношению прилежащего катета OA к гипотенузе MA, то есть \(\cos \angle A = \frac{OA}{MA} = \frac{r}{l}\). По условию, диаметр основания конуса \(d_0\) равен образующей \(l\), а диаметр основания \(d_0\) равен двум радиусам \(2r\). Следовательно, \(l = d_0 = 2r\). Подставляя это в выражение для косинуса, получаем \(\cos \angle A = \frac{r}{2r} = \frac{1}{2}\). Из этого следует, что угол A равен \(60^\circ\). В том же прямоугольном треугольнике MOA тангенс угла A равен отношению противолежащего катета MO к прилежащему катету OA, то есть \(\tan \angle A = \frac{MO}{OA} = \frac{h}{r}\). Поскольку \(\angle A = 60^\circ\), \(\tan 60^\circ = \frac{h}{r}\). Известно, что \(\tan 60^\circ = \sqrt{3}\), поэтому \(\sqrt{3} = \frac{h}{r}\). Выразим радиус основания конуса через его высоту: \(r = \frac{h}{\sqrt{3}}\).

Площадь основания конуса \(S_{\text{осн}}\) вычисляется по формуле площади круга: \(S_{\text{осн}} = \pi r^2\). Подставим найденное значение радиуса: \(S_{\text{осн}} = \pi \left(\frac{h}{\sqrt{3}}\right)^2 = \pi \frac{h^2}{3} = \frac{\pi h^2}{3}\).

Образующая конуса \(l\) по условию равна диаметру основания \(d_0\), который равен \(2r\). Следовательно, \(l = 2r\). Подставим выражение для \(r\) через \(h\): \(l = 2 \cdot \frac{h}{\sqrt{3}} = \frac{2h}{\sqrt{3}}\).

Площадь боковой поверхности конуса \(S_{\text{бок}}\) вычисляется по формуле \(S_{\text{бок}} = \pi r l\). Подставим выражения для \(r\) и \(l\) через \(h\): \(S_{\text{бок}} = \pi \cdot \frac{h}{\sqrt{3}} \cdot \frac{2h}{\sqrt{3}} = \pi \cdot \frac{2h^2}{(\sqrt{3})^2} = \pi \cdot \frac{2h^2}{3} = \frac{2\pi h^2}{3}\).

Полная площадь поверхности конуса \(S_{\text{конуса}}\) равна сумме площади основания и площади боковой поверхности: \(S_{\text{конуса}} = S_{\text{осн}} + S_{\text{бок}}\). Подставим найденные значения: \(S_{\text{конуса}} = \frac{\pi h^2}{3} + \frac{2\pi h^2}{3} = \frac{\pi h^2 + 2\pi h^2}{3} = \frac{3\pi h^2}{3} = \pi h^2\).

Площадь сферы \(S_{\text{сферы}}\) вычисляется по формуле \(S_{\text{сферы}} = 4 \pi R^2\), где \(R\) — радиус сферы. По условию, диаметр сферы \(d\) равен высоте конуса \(h\), то есть \(d = h\). Радиус сферы равен половине ее диаметра: \(R = \frac{d}{2}\). Подставим \(d = h\): \(R = \frac{h}{2}\). Теперь подставим радиус сферы в формулу площади сферы: \(S_{\text{сферы}} = 4 \pi \left(\frac{h}{2}\right)^2 = 4 \pi \frac{h^2}{4} = \pi h^2\).

Сравнивая полную площадь поверхности конуса \(S_{\text{конуса}} = \pi h^2\) и площадь сферы \(S_{\text{сферы}} = \pi h^2\), видим, что они равны. Таким образом, \(S_{\text{конуса}} = S_{\text{сферы}}\), что и требовалось доказать.