
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 514 Атанасян — Подробные Ответы
Круговой сектор с углом 30° и радиусом \(R\) вращается вокруг одного из ограничивающих его радиусов. Найдите объём получившегося шарового сектора.
Дано: угол сектора \(\alpha = 30^\circ\), радиус \(R\). Найти: объем \(V\) получившегося тела вращения. При вращении кругового сектора вокруг радиуса \(OB\), углы \(\angle COB\) и \(\angle BOA\) равны \(30^\circ\), что дает \(\angle COA = 60^\circ\). Поскольку \(CO = OA = R\), треугольник \(\triangle COA\) является равносторонним, следовательно, \(CA = R\). В прямоугольном треугольнике \(\triangle CDO\), где \(CD = \frac{CA}{2} = \frac{R}{2}\) и \(CO = R\), находим \(OD = \sqrt{CO^2 — CD^2} = \sqrt{R^2 — (\frac{R}{2})^2} = \sqrt{R^2 — \frac{R^2}{4}} = \sqrt{\frac{3R^2}{4}} = \frac{R\sqrt{3}}{2}\). Высота \(h\) шарового сектора равна \(DB = OB — OD = R — \frac{R\sqrt{3}}{2} = R(1 — \frac{\sqrt{3}}{2})\). Объем шарового сектора вычисляется по формуле \(V = \frac{2}{3}\pi R^2 h\). Подставляя значение \(h\), получаем \(V = \frac{2}{3}\pi R^2 \left(R(1 — \frac{\sqrt{3}}{2})\right) = \frac{2}{3}\pi R^3 (1 — \frac{\sqrt{3}}{2}) = \frac{2}{3}\pi R^3 — \frac{2}{3}\pi R^3 \frac{\sqrt{3}}{2} =\)
\(=\frac{2}{3}\pi R^3 — \frac{\sqrt{3}}{3}\pi R^3 = \frac{2-\sqrt{3}}{3}\pi R^3\). Ответ: \(V = \frac{2-\sqrt{3}}{3}\pi R^3\).
Дано: круговой сектор \(OAB\) с углом \(\alpha = 30^\circ\) и радиусом \(R\). Сектор вращается вокруг радиуса \(OB\). Найти: объем \(V\) полученного тела вращения.
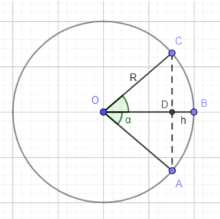
Первый шаг — понять геометрию вращения. Когда круговой сектор \(OAB\) вращается вокруг радиуса \(OB\), точка \(A\) описывает окружность, а сектор формирует шаровой сектор. Угол сектора \(\angle AOB\) равен \(30^\circ\). По условию, вращение происходит вокруг радиуса \(OB\). В результате вращения точка \(C\) симметрична точке \(A\) относительно оси вращения \(OB\), и угол \(\angle COB\) также равен \(30^\circ\). Таким образом, полный угол \(\angle COA\) равен \(\angle COB + \angle BOA = 30^\circ + 30^\circ = 60^\circ\).
Второй шаг — рассмотреть треугольник \(\triangle COA\). У нас есть \(\angle COA = 60^\circ\) и стороны \(CO = OA = R\) (так как это радиусы исходного кругового сектора). Поскольку это равнобедренный треугольник с углом \(60^\circ\) при вершине \(O\), он является равносторонним. Следовательно, сторона \(CA\) также равна \(R\).
Третий шаг — найти высоту треугольника \(\triangle COA\) относительно стороны \(CA\). Пусть \(D\) — середина отрезка \(CA\). Тогда \(OD\) является высотой, медианой и биссектрисой в равностороннем треугольнике \(\triangle COA\). В прямоугольном треугольнике \(\triangle CDO\), катет \(CD\) равен половине стороны \(CA\), то есть \(CD = \frac{CA}{2} = \frac{R}{2}\). Гипотенуза \(CO\) равна \(R\). По теореме Пифагора, \(OD^2 + CD^2 = CO^2\). Отсюда \(OD^2 = CO^2 — CD^2 = R^2 — \left(\frac{R}{2}\right)^2 = R^2 — \frac{R^2}{4} = \frac{4R^2 — R^2}{4} = \frac{3R^2}{4}\). Извлекая квадратный корень, получаем \(OD = \sqrt{\frac{3R^2}{4}} = \frac{\sqrt{3R^2}}{\sqrt{4}} = \frac{R\sqrt{3}}{2}\).
Четвертый шаг — определить высоту \(h\) получившегося шарового сегмента. Шаровой сегмент образуется вращением части кругового сектора. Его высота \(h\) — это расстояние от вершины \(B\) (на оси вращения) до основания сегмента (окружности, описанной точкой \(A\)). Основание сегмента лежит в плоскости, проходящей через точку \(D\) перпендикулярно оси \(OB\). Таким образом, высота \(h\) равна расстоянию \(DB\). Точка \(B\) находится на расстоянии \(R\) от \(O\) (\(OB = R\)). Точка \(D\) находится на расстоянии \(OD = \frac{R\sqrt{3}}{2}\) от \(O\) вдоль той же оси \(OB\). Следовательно, высота \(h = DB = OB — OD = R — \frac{R\sqrt{3}}{2}\). Эту высоту можно записать как \(h = R\left(1 — \frac{\sqrt{3}}{2}\right)\).
Пятый шаг — вычислить объем \(V\) шарового сегмента. Объем шарового сегмента с одной основой вычисляется по формуле \(V = \frac{1}{3}\pi h^2 (3R — h)\), где \(R\) — радиус шара, а \(h\) — высота сегмента. Однако, в данном случае, тело вращения является шаровым сектором, который образуется вращением кругового сектора. Объем шарового сектора вычисляется по формуле \(V = \frac{2}{3}\pi R^2 h\), где \(R\) — радиус шара (равный радиусу исходного сектора), а \(h\) — высота соответствующего шарового сегмента. Мы уже нашли \(h = R\left(1 — \frac{\sqrt{3}}{2}\right)\).
Подставляем значение \(h\) в формулу объема шарового сектора: \(V = \frac{2}{3}\pi R^2 \left(R\left(1 — \frac{\sqrt{3}}{2}\right)\right)\). Раскрываем скобки: \(V = \frac{2}{3}\pi R^3 \left(1 — \frac{\sqrt{3}}{2}\right)\). Умножаем: \(V = \frac{2}{3}\pi R^3 \cdot 1 — \frac{2}{3}\pi R^3 \cdot \frac{\sqrt{3}}{2}\). Сокращаем: \(V = \frac{2}{3}\pi R^3 — \frac{\sqrt{3}}{3}\pi R^3\). Выносим общий множитель \(\frac{\pi R^3}{3}\): \(V = \frac{\pi R^3}{3} (2 — \sqrt{3})\). Или, как в примере, \(V = \frac{2-\sqrt{3}}{3}\pi R^3\).
Таким образом, объем получившегося шарового сектора равен \(\frac{2-\sqrt{3}}{3}\pi R^3\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!