
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 512 Атанасян — Подробные Ответы
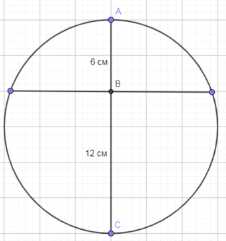
В шаре проведена плоскость, перпендикулярная к диаметру и делящая его на части 6 см и 12 см. Найдите объёмы двух полученных частей шара.
Диаметр шара равен сумме длин частей, на которые он делится плоскостью: \(d = 6 + 12 = 18\) см. Радиус шара равен половине диаметра: \(R = \frac{18}{2} = 9\) см.
Объем первого шарового сегмента с высотой \(h_1 = 6\) см и радиусом шара \(R = 9\) см находится по формуле \(V = \frac{1}{3}\pi h^2 (3R — h)\):
\(V_1 = \frac{1}{3}\pi (6)^2 (3 \cdot 9 — 6) = \frac{1}{3}\pi \cdot 36 (27 — 6) = 12\pi \cdot 21 = 252\pi\) см³.
Объем второго шарового сегмента с высотой \(h_2 = 12\) см и радиусом шара \(R = 9\) см находится по формуле \(V = \frac{1}{3}\pi h^2 (3R — h)\):
\(V_2 = \frac{1}{3}\pi (12)^2 (3 \cdot 9 — 12) = \frac{1}{3}\pi \cdot 144 (27 — 12) = 48\pi \cdot 15 = 720\pi\) см³.
Ответ: \(V_1 = 252\pi\) см³; \(V_2 = 720\pi\) см³.
Диаметр шара \(d\) равен сумме длин двух отрезков, на которые плоскость делит диаметр. В данном случае эти отрезки имеют длины 6 см и 12 см. Следовательно, диаметр шара составляет \(d = 6 + 12 = 18\) см.
Радиус шара \(R\) равен половине его диаметра. Таким образом, радиус шара равен \(R = \frac{d}{2} = \frac{18}{2} = 9\) см.
Плоскость, перпендикулярная диаметру, делит шар на два шаровых сегмента. Высота первого шарового сегмента \(h_1\) равна длине одного из отрезков диаметра, то есть \(h_1 = 6\) см. Высота второго шарового сегмента \(h_2\) равна длине другого отрезка диаметра, то есть \(h_2 = 12\) см.
Объем шарового сегмента с высотой \(h\) и радиусом шара \(R\) вычисляется по формуле \(V = \frac{1}{3}\pi h^2 (3R — h)\).
Найдем объем первого шарового сегмента с высотой \(h_1 = 6\) см и радиусом шара \(R = 9\) см. Подставим эти значения в формулу объема шарового сегмента:
\(V_1 = \frac{1}{3}\pi (6)^2 (3 \cdot 9 — 6)\).
Сначала вычислим квадрат высоты: \((6)^2 = 36\).
Затем вычислим выражение в скобках: \(3 \cdot 9 — 6 = 27 — 6 = 21\).
Теперь подставим эти значения обратно в формулу:
\(V_1 = \frac{1}{3}\pi \cdot 36 \cdot 21\).
Умножим \(\frac{1}{3}\) на 36: \(\frac{1}{3} \cdot 36 = 12\).
Теперь умножим результат на \(\pi\) и 21: \(V_1 = 12\pi \cdot 21\).
Выполним умножение 12 на 21: \(12 \cdot 21 = 252\).
Таким образом, объем первого шарового сегмента равен \(V_1 = 252\pi\) см³.
Теперь найдем объем второго шарового сегмента с высотой \(h_2 = 12\) см и радиусом шара \(R = 9\) см. Подставим эти значения в формулу объема шарового сегмента:
\(V_2 = \frac{1}{3}\pi (12)^2 (3 \cdot 9 — 12)\).
Сначала вычислим квадрат высоты: \((12)^2 = 144\).
Затем вычислим выражение в скобках: \(3 \cdot 9 — 12 = 27 — 12 = 15\).
Теперь подставим эти значения обратно в формулу:
\(V_2 = \frac{1}{3}\pi \cdot 144 \cdot 15\).
Умножим \(\frac{1}{3}\) на 144: \(\frac{1}{3} \cdot 144 = 48\).
Теперь умножим результат на \(\pi\) и 15: \(V_2 = 48\pi \cdot 15\).
Выполним умножение 48 на 15: \(48 \cdot 15 = 720\).
Таким образом, объем второго шарового сегмента равен \(V_2 = 720\pi\) см³.
Ответ: Объемы двух полученных частей шара равны \(V_1 = 252\pi\) см³ и \(V_2 = 720\pi\) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!