ГДЗ по Геометрии 11 класс Номер 511 Атанасян — Подробные Ответы

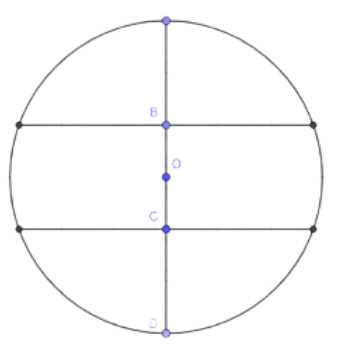
Диаметр шара разделён на три равные части и через точки деления проведены плоскости, перпендикулярные к диаметру. Найдите объём получившегося шарового слоя, если радиус шара равен \(R\).

Высота каждого из двух крайних сегментов равна \(h = \frac{2}{3}R\).
Суммарный объем крайних сегментов равен \(V_{сег} = 2 \cdot \frac{1}{3}\pi h^2 (3R — h) = 2 \cdot \frac{1}{3}\pi (\frac{2}{3}R)^2 (3R — \frac{2}{3}R) = \frac{56}{81}\pi R^3\).
Объем шара равен \(V_{шара} = \frac{4}{3}\pi R^3\).
Объем шарового слоя равен \(V_{слоя} = V_{шара} — V_{сег} = \frac{4}{3}\pi R^3 — \frac{56}{81}\pi R^3 = \frac{108}{81}\pi R^3 — \frac{56}{81}\pi R^3 = \frac{52}{81}\pi R^3\).
Ответ: \(V_{слоя} = \frac{52}{81}\pi R^3\) см³.

Диаметр шара, равный \(2R\), разделен на три равные части плоскостями, перпендикулярными диаметру. Это означает, что каждая из трех частей диаметра имеет длину \(\frac{2R}{3}\). Шаровой слой образуется между двумя внутренними плоскостями, а два шаровых сегмента отсекаются внешними плоскостями. Высота каждого из этих двух крайних шаровых сегментов равна длине одной из крайних частей диаметра, то есть \(h = \frac{2R}{3}\).

Объем шарового сегмента высотой \(h\) и радиусом шара \(R\) определяется формулой \(V_{сегмент} = \frac{1}{3}\pi h^2 (3R — h)\). Поскольку у нас два одинаковых крайних сегмента, их суммарный объем будет в два раза больше объема одного сегмента. Подставим значение высоты \(h = \frac{2R}{3}\) в формулу для объема одного сегмента:
\(V_{сегмент} = \frac{1}{3}\pi (\frac{2R}{3})^2 (3R — \frac{2R}{3}) = \frac{1}{3}\pi \frac{4R^2}{9} (\frac{9R — 2R}{3}) = \frac{1}{3}\pi \frac{4R^2}{9} \frac{7R}{3} = \frac{28}{81}\pi R^3\).
Суммарный объем двух крайних сегментов равен \(V_{крайних\ сегментов} = 2 \cdot V_{сегмент} = 2 \cdot \frac{28}{81}\pi R^3 = \frac{56}{81}\pi R^3\).

Объем всего шара радиусом \(R\) определяется формулой \(V_{шара} = \frac{4}{3}\pi R^3\).

Шаровой слой, получившийся в результате деления диаметра на три равные части, представляет собой часть шара между двумя крайними сегментами. Следовательно, объем шарового слоя можно найти как разность между объемом всего шара и суммарным объемом двух крайних сегментов.
\(V_{слоя} = V_{шара} — V_{крайних\ сегментов} = \frac{4}{3}\pi R^3 — \frac{56}{81}\pi R^3\).
Чтобы выполнить вычитание, приведем дроби к общему знаменателю 81:
\(\frac{4}{3}\pi R^3 = \frac{4 \cdot 27}{3 \cdot 27}\pi R^3 = \frac{108}{81}\pi R^3\).
Теперь вычтем:
\(V_{слоя} = \frac{108}{81}\pi R^3 — \frac{56}{81}\pi R^3 = \frac{108 — 56}{81}\pi R^3 = \frac{52}{81}\pi R^3\).

Таким образом, объем получившегося шарового слоя равен \(\frac{52}{81}\pi R^3\).
Ответ: Объем шарового слоя равен \(\frac{52}{81}\pi R^3\) см³.