ГДЗ по Геометрии 11 класс Номер 510 Атанасян — Подробные Ответы

Найдите объём шарового сегмента, если радиус окружности его основания равен 60 см, а радиус шара равен 75 см.

Дано: \(r = 60\) см; \(R = 75\) см.
Решение:
Рассмотрим прямоугольный треугольник с гипотенузой \(R\), одним катетом \(r\) и другим катетом \(R — h\). По теореме Пифагора имеем \(R^2 = (R — h)^2 + r^2\).
Раскрывая скобки, получаем \(R^2 = R^2 — 2Rh + h^2 + r^2\).
Отсюда следует квадратное уравнение относительно \(h\): \(h^2 — 2Rh + r^2 = 0\).
Подставляя значения \(R = 75\) и \(r = 60\), получаем \(h^2 — 2(75)h + 60^2 = 0\), что упрощается до \(h^2 — 150h + 3600 = 0\).
Решая это квадратное уравнение, находим две возможные высоты сегмента: \(h_1 = 30\) см и \(h_2 = 120\) см.
Объем шарового сегмента находится по формуле \(V = \pi h^2 (R — \frac{1}{3}h)\).
Для \(h_1 = 30\) см: \(V_1 = \pi (30)^2 (75 — \frac{1}{3}(30)) = 900\pi (75 — 10) = 900\pi \cdot 65 = 58500\pi\) см³.
Для \(h_2 = 120\) см: \(V_2 = \pi (120)^2 (75 — \frac{1}{3}(120)) = 14400\pi (75 — 40) = 14400\pi \cdot 35 = 504000\pi\) см³.
Ответ: \(58500\pi\) см³ или \(504000\pi\) см³.

Дано: радиус окружности основания шарового сегмента \(r = 60\) см, радиус шара \(R = 75\) см.
Найти: объем шарового сегмента.

Решение:
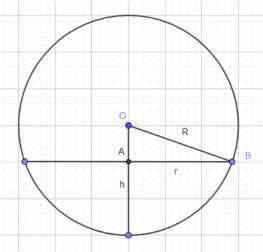
Рассмотрим осевое сечение шара и шарового сегмента. В этом сечении окружность основания сегмента представляет собой хорду шара, перпендикулярную диаметру. Радиус этой хорды равен \(r\). Центр шара обозначим \(O\). Пусть \(A\) и \(B\) — точки пересечения окружности основания сегмента с окружностью шара, а \(C\) — центр окружности основания сегмента. Тогда \(CA = CB = r\). Расстояние от центра шара до центра основания сегмента обозначим через \(d\). Высота шарового сегмента \(h\) может быть выражена как \(h = R — d\) или \(h = R + d\), в зависимости от того, где находится центр основания относительно центра шара. В данном случае, судя по чертежу и дальнейшему решению, рассматривается сегмент, где центр основания находится между центром шара и вершиной сегмента, поэтому \(d = R — h\).

Рассмотрим прямоугольный треугольник, образованный радиусом шара \(OB = R\), радиусом основания сегмента \(AB = r\) (в сечении это половина хорды \(AB\), то есть \(CB = r\)) и расстоянием от центра шара до центра основания сегмента \(OA = d\). В данном случае, на чертеже точка \(A\) является центром основания сегмента, и расстояние от \(O\) до \(A\) равно \(R — h\). Таким образом, в прямоугольном треугольнике \(OAB\), где \(OB\) — гипотенуза, \(OA\) и \(AB\) — катеты, по теореме Пифагора имеем:
\(OB^2 = OA^2 + AB^2\)
\(R^2 = (R — h)^2 + r^2\)

Раскроем скобки в выражении \((R — h)^2\):
\(R^2 = R^2 — 2Rh + h^2 + r^2\)

Перенесем все слагаемые в одну сторону, чтобы получить квадратное уравнение относительно \(h\):
\(R^2 — R^2 + 2Rh — h^2 — r^2 = 0\)
\(2Rh — h^2 — r^2 = 0\)
Умножим на \(-1\) для удобства:
\(h^2 — 2Rh + r^2 = 0\)

Теперь подставим известные значения \(R = 75\) см и \(r = 60\) см в это уравнение:
\(h^2 — 2(75)h + (60)^2 = 0\)
\(h^2 — 150h + 3600 = 0\)

Решим это квадратное уравнение для нахождения высоты \(h\). Используем формулу для корней квадратного уравнения \(h = \frac{-b \pm \sqrt{b^2 — 4ac}}{2a}\), где \(a=1\), \(b=-150\), \(c=3600\).
Дискриминант \(D = b^2 — 4ac = (-150)^2 — 4(1)(3600) = 22500 — 14400 = 8100\).
\(\sqrt{D} = \sqrt{8100} = 90\).

Находим корни уравнения:
\(h_1 = \frac{-(-150) + 90}{2(1)} = \frac{150 + 90}{2} = \frac{240}{2} = 120\)
\(h_2 = \frac{-(-150) — 90}{2(1)} = \frac{150 — 90}{2} = \frac{60}{2} = 30\)

Таким образом, мы получаем две возможные высоты для шарового сегмента: \(h_1 = 120\) см и \(h_2 = 30\) см. Это связано с тем, что при данном радиусе основания \(r\) и радиусе шара \(R\) может существовать два шаровых сегмента с таким основанием — один «маленький» и один «большой».

Теперь найдем объем шарового сегмента, используя формулу \(V = \pi h^2 (R — \frac{1}{3}h)\).

Для первой высоты \(h_1 = 30\) см:
\(V_1 = \pi (30)^2 (75 — \frac{1}{3}(30))\)
\(V_1 = \pi (900) (75 — 10)\)
\(V_1 = 900\pi (65)\)
\(V_1 = 58500\pi\) см³

Для второй высоты \(h_2 = 120\) см:
\(V_2 = \pi (120)^2 (75 — \frac{1}{3}(120))\)
\(V_2 = \pi (14400) (75 — 40)\)
\(V_2 = 14400\pi (35)\)
\(V_2 = 504000\pi\) см³

Ответ: Объем шарового сегмента может составлять \(58500\pi\) см³ или \(504000\pi\) см³.