ГДЗ по Геометрии 11 класс Номер 509 Атанасян — Подробные Ответы

Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объём общей части шаров к объёму одного шара?

Четырехугольник \(O_1AO_2B\) является ромбом со стороной \(R\), откуда следует, что \(AB \perp O_1O_2\) и \(O_1C = CO_2 = R/2\). Общая часть шаров представляет собой два одинаковых шаровых сегмента высотой \(h = R/2\). Объем одного шарового сегмента равен \(V_{сегмента} = \pi h^2 (R — \frac{1}{3}h)\). Подставляя значение \(h\), получаем \(V_{сегмента} = \pi (\frac{R}{2})^2 (R — \frac{1}{3}\frac{R}{2}) = \pi \frac{R^2}{4} (R — \frac{R}{6}) = \pi \frac{R^2}{4} \frac{5R}{6} = \frac{5\pi R^3}{24}\). Общий объем двух сегментов равен \(V_{общ} = 2 \cdot V_{сегмента} = 2 \cdot \frac{5\pi R^3}{24} = \frac{5\pi R^3}{12}\). Объем одного шара равен \(V_1 = \frac{4}{3}\pi R^3\). Отношение общего объема к объему одного шара составляет \(\frac{V_{общ}}{V_1} = \frac{5\pi R^3 / 12}{4\pi R^3 / 3} = \frac{5\pi R^3}{12} \cdot \frac{3}{4\pi R^3} = \frac{15}{48} = \frac{5}{16}\). Ответ: 5 : 16.

Дано два равных шара с центрами \(O_1\) и \(O_2\) и радиусами \(R_1 = R_2 = R\). По условию, центр одного шара лежит на поверхности другого, что означает, что расстояние между центрами шаров равно их радиусу, то есть \(O_1O_2 = R\).

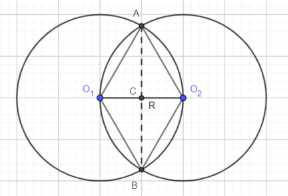
Рассмотрим сечение шаров плоскостью, проходящей через центры \(O_1\) и \(O_2\). В этом сечении мы увидим две окружности радиуса \(R\), центры которых находятся на расстоянии \(R\) друг от друга. Точки пересечения этих окружностей обозначим \(A\) и \(B\). Соединив центры и точки пересечения, получим четырехугольник \(O_1AO_2B\). Все стороны этого четырехугольника равны радиусу \(R\), так как \(O_1A = O_1B = R\) (радиусы первого шара) и \(O_2A = O_2B = R\) (радиусы второго шара). Следовательно, четырехугольник \(O_1AO_2B\) является ромбом.

Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Диагоналями ромба \(O_1AO_2B\) являются отрезки \(AB\) и \(O_1O_2\). Пусть \(C\) — точка пересечения диагоналей. Тогда \(AB \perp O_1O_2\), и точка \(C\) является серединой отрезка \(O_1O_2\). Поскольку \(O_1O_2 = R\), то \(O_1C = CO_2 = \frac{R}{2}\).

Общая часть двух пересекающихся шаров представляет собой тело, составленное из двух одинаковых шаровых сегментов. Каждый сегмент отсекается от своего шара плоскостью, проходящей через общую окружность пересечения (с центром в точке \(C\) и радиусом \(AC\)). Высота каждого шарового сегмента — это расстояние от центра соответствующего шара до плоскости сечения. Для первого шара высота сегмента равна \(h_1 = O_1C = \frac{R}{2}\). Для второго шара высота сегмента равна \(h_2 = O_2C = \frac{R}{2}\). Таким образом, оба сегмента имеют одинаковую высоту \(h = \frac{R}{2}\).

Объем шарового сегмента вычисляется по формуле \(V_{сегмента} = \pi h^2 (R — \frac{1}{3}h)\), где \(R\) — радиус шара, а \(h\) — высота сегмента. Подставим значение высоты \(h = \frac{R}{2}\) в формулу объема сегмента:
\(V_{сегмента} = \pi \left(\frac{R}{2}\right)^2 \left(R — \frac{1}{3}\left(\frac{R}{2}\right)\right)\)
\(V_{сегмента} = \pi \frac{R^2}{4} \left(R — \frac{R}{6}\right)\)
Для вычисления выражения в скобках приведем к общему знаменателю: \(R — \frac{R}{6} = \frac{6R}{6} — \frac{R}{6} = \frac{5R}{6}\).
Теперь подставим это обратно в формулу объема сегмента:
\(V_{сегмента} = \pi \frac{R^2}{4} \left(\frac{5R}{6}\right)\)
\(V_{сегмента} = \frac{5\pi R^3}{24}\).

Общая часть шаров состоит из двух таких одинаковых сегментов, поэтому ее объем \(V_{общ}\) равен удвоенному объему одного сегмента:
\(V_{общ} = 2 \cdot V_{сегмента} = 2 \cdot \frac{5\pi R^3}{24} = \frac{10\pi R^3}{24}\).
Сократим дробь \(\frac{10}{24}\) на 2: \(\frac{10}{24} = \frac{5}{12}\).
Таким образом, объем общей части шаров равен \(V_{общ} = \frac{5\pi R^3}{12}\).

Объем одного шара с радиусом \(R\) вычисляется по формуле \(V_1 = \frac{4}{3}\pi R^3\).

Нам необходимо найти отношение объема общей части шаров к объему одного шара, то есть \(\frac{V_{общ}}{V_1}\).
\(\frac{V_{общ}}{V_1} = \frac{\frac{5\pi R^3}{12}}{\frac{4}{3}\pi R^3}\).
Чтобы разделить две дроби, умножим первую дробь на обратную второй:
\(\frac{V_{общ}}{V_1} = \frac{5\pi R^3}{12} \cdot \frac{3}{4\pi R^3}\).
Сократим \(\pi R^3\) в числителе и знаменателе:
\(\frac{V_{общ}}{V_1} = \frac{5}{12} \cdot \frac{3}{4}\).
Умножим числители и знаменатели:
\(\frac{V_{общ}}{V_1} = \frac{5 \cdot 3}{12 \cdot 4} = \frac{15}{48}\).
Сократим дробь \(\frac{15}{48}\) на наибольший общий делитель 3:
\(\frac{15 \div 3}{48 \div 3} = \frac{5}{16}\).

Таким образом, отношение объема общей части шаров к объему одного шара составляет \(5:16\).