ГДЗ по Геометрии 11 класс Номер 508 Атанасян — Подробные Ответы

Сколько кубометров земли потребуется для устройства клумбы, имеющей форму шарового сегмента с радиусом основания 5 м и высотой 60 см?

Дано: радиус основания шарового сегмента \(r = 5\) м, высота шарового сегмента \(h = 0.6\) м.
Найдем радиус сферы \(R\). Из прямоугольного треугольника, образованного радиусом сферы \(R\), радиусом основания сегмента \(r\) и расстоянием от центра сферы до основания сегмента \(R-h\), по теореме Пифагора имеем \(R^2 = (R-h)^2 + r^2\). Раскрывая скобки, получаем \(R^2 = R^2 — 2Rh + h^2 + r^2\). Отсюда \(2Rh = h^2 + r^2\), и \(R = \frac{h^2 + r^2}{2h}\). Подставляя значения, \(R = \frac{(0.6)^2 + 5^2}{2 \cdot 0.6} = \frac{0.36 + 25}{1.2} = \frac{25.36}{1.2} = \frac{2536}{120} = \frac{317}{15}\) м.
Объем шарового сегмента вычисляется по формуле \(V = \pi h^2 \left(R — \frac{1}{3}h\right)\).
Подставим значения \(h = 0.6\) и \(R = \frac{317}{15}\) в формулу объема: \(V = \pi (0.6)^2 \left(\frac{317}{15} — \frac{1}{3}(0.6)\right) = \pi (0.36) \left(\frac{317}{15} — 0.2\right)\). Преобразуем десятичные дроби в обыкновенные: \(0.36 = \frac{36}{100} = \frac{9}{25}\) и \(0.2 = \frac{2}{10} = \frac{1}{5}\).
\(V = \pi \cdot \frac{9}{25} \left(\frac{317}{15} — \frac{1}{5}\right)\). Приведем дроби в скобках к общему знаменателю 15: \(V = \pi \cdot \frac{9}{25} \left(\frac{317}{15} — \frac{3}{15}\right) = \pi \cdot \frac{9}{25} \cdot \frac{314}{15}\).
Умножим числители и знаменатели и сократим: \(V = \pi \cdot \frac{9 \cdot 314}{25 \cdot 15} = \pi \cdot \frac{3 \cdot 314}{25 \cdot 5} = \pi \cdot \frac{942}{125}\).
Объем клумбы составляет \(\frac{942}{125}\pi\) м³.

Ответ: \(V = \frac{942}{125}\pi\) м².

Для устройства клумбы, имеющей форму шарового сегмента, потребуется объем земли, равный объему этого шарового сегмента. Нам даны радиус основания шарового сегмента \(r = 5\) м и его высота \(h = 0.6\) м. Чтобы найти объем шарового сегмента, нам сначала нужно определить радиус сферы \(R\), частью которой является этот сегмент.

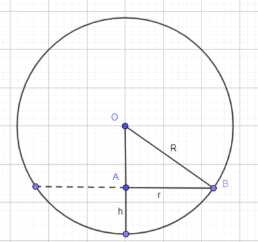
Представим вертикальное сечение сферы, проходящее через ее центр и центр основания шарового сегмента. В этом сечении основание сегмента будет представлять собой хорду, а высота сегмента — перпендикуляр от высшей точки сегмента до центра основания. Соединив центр сферы с любой точкой на окружности основания сегмента, мы получим радиус сферы \(R\). Расстояние от центра сферы до центра основания сегмента будет равно \(R-h\). Таким образом, образуется прямоугольный треугольник с катетами \(r\) и \(R-h\), и гипотенузой \(R\).

По теореме Пифагора для этого прямоугольного треугольника справедливо соотношение \(R^2 = (R-h)^2 + r^2\). Раскроем скобки в правой части уравнения: \(R^2 = R^2 — 2Rh + h^2 + r^2\). Вычтем \(R^2\) из обеих частей: \(0 = -2Rh + h^2 + r^2\). Перенесем член с \(R\) в левую часть: \(2Rh = h^2 + r^2\). Теперь выразим радиус сферы \(R\): \(R = \frac{h^2 + r^2}{2h}\).

Подставим известные значения \(h = 0.6\) м и \(r = 5\) м: \(R = \frac{(0.6)^2 + 5^2}{2 \cdot 0.6}\). Вычислим квадраты: \(0.6^2 = 0.36\) и \(5^2 = 25\). Знаменатель равен \(2 \cdot 0.6 = 1.2\). Таким образом, \(R = \frac{0.36 + 25}{1.2} = \frac{25.36}{1.2}\). Чтобы упростить дробь, умножим числитель и знаменатель на 100: \(R = \frac{2536}{120}\). Сократим эту дробь. Оба числа делятся на 8: \(2536 \div 8 = 317\) и \(120 \div 8 = 15\). Следовательно, радиус сферы \(R = \frac{317}{15}\) м.

Теперь, зная радиус сферы \(R\) и высоту шарового сегмента \(h\), мы можем вычислить объем шарового сегмента по формуле \(V = \pi h^2 \left(R — \frac{1}{3}h\right)\).

Подставим значения \(h = 0.6\) и \(R = \frac{317}{15}\) в формулу объема: \(V = \pi (0.6)^2 \left(\frac{317}{15} — \frac{1}{3}(0.6)\right)\). Вычислим \(h^2 = (0.6)^2 = 0.36\). Вычислим \(\frac{1}{3}h = \frac{1}{3}(0.6) = 0.2\). Теперь выражение для объема выглядит так: \(V = \pi (0.36) \left(\frac{317}{15} — 0.2\right)\).

Для удобства дальнейших вычислений представим десятичные дроби в виде обыкновенных: \(0.36 = \frac{36}{100} = \frac{9}{25}\) и \(0.2 = \frac{2}{10} = \frac{1}{5}\). Подставим эти дроби в формулу объема: \(V = \pi \cdot \frac{9}{25} \left(\frac{317}{15} — \frac{1}{5}\right)\).

Выполним вычитание в скобках, приведя дроби к общему знаменателю 15: \(\frac{317}{15} — \frac{1}{5} = \frac{317}{15} — \frac{1 \cdot 3}{5 \cdot 3} = \frac{317}{15} — \frac{3}{15} = \frac{317 — 3}{15} = \frac{314}{15}\).

Теперь подставим результат вычитания обратно в формулу объема: \(V = \pi \cdot \frac{9}{25} \cdot \frac{314}{15}\). Умножим числители и знаменатели: \(V = \pi \cdot \frac{9 \cdot 314}{25 \cdot 15}\). Сократим дробь, заметив, что 9 и 15 имеют общий множитель 3: \(9 \div 3 = 3\) и \(15 \div 3 = 5\). Получаем: \(V = \pi \cdot \frac{3 \cdot 314}{25 \cdot 5}\). Выполним умножение в числителе и знаменателе: \(3 \cdot 314 = 942\) и \(25 \cdot 5 = 125\).

Таким образом, объем шарового сегмента равен \(V = \pi \cdot \frac{942}{125} = \frac{942}{125}\pi\) м³. Этот объем соответствует количеству земли, необходимому для устройства клумбы.

Ответ: объем земли, необходимый для устройства клумбы, составляет \(\frac{942}{125}\pi\) м³.