ГДЗ по Геометрии 11 класс Номер 502 Атанасян — Подробные Ответы

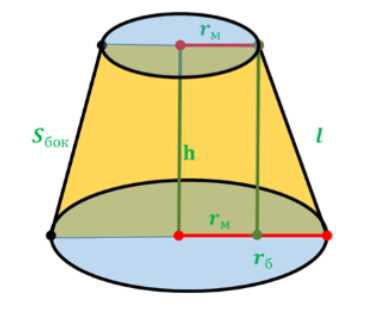
В усечённом конусе известны высота \(h\), образующая \(l\) и площадь \(S\) боковой поверхности. Найдите площадь осевого сечения и объём усечённого конуса.

Площадь осевого сечения усечённого конуса равна произведению полусуммы диаметров оснований на высоту, что эквивалентно произведению полусуммы радиусов оснований на удвоенную высоту, или произведению суммы радиусов оснований на высоту: \(S_{сеч} = (r_б + r_м) h\). Из формулы площади боковой поверхности \(S = \pi (r_б + r_м) l\) следует, что \(r_б + r_м = \frac{S}{\pi l}\). Подставляя это выражение в формулу площади осевого сечения, получаем \(S_{сеч} = \frac{S h}{\pi l}\).

Для нахождения объёма усечённого конуса \(V = \frac{1}{3} \pi h (r_б^2 + r_м^2 + r_б r_м)\) необходимо найти выражения для радиусов \(r_б\) и \(r_м\). Используя теорему Пифагора для прямоугольного треугольника, образованного высотой, образующей и разностью радиусов, имеем \(h^2 + (r_б — r_м)^2 = l^2\), откуда \(r_б — r_м = \sqrt{l^2 — h^2}\). Решая систему уравнений \(r_б + r_м = \frac{S}{\pi l}\) и \(r_б — r_м = \sqrt{l^2 — h^2}\), находим \(r_б = \frac{1}{2} \left( \frac{S}{\pi l} + \sqrt{l^2 — h^2} \right)\) и \(r_м = \frac{1}{2} \left( \frac{S}{\pi l} — \sqrt{l^2 — h^2} \right)\). Подставляя эти выражения в формулу объёма и выполняя преобразования, получаем \(V = \frac{h S^2}{4 \pi l^2} + \frac{\pi h (l^2 — h^2)}{12}\).

Ответ: площадь осевого сечения \(S_{сеч} = \frac{S h}{\pi l}\), объём усечённого конуса \(V = \frac{h S^2}{4 \pi l^2} + \frac{\pi h (l^2 — h^2)}{12}\).

Дано усеченный конус с высотой \(h\), образующей \(l\) и площадью боковой поверхности \(S\). Требуется найти объем \(V\) усеченного конуса и площадь \(S_{сеч}\) его осевого сечения.

Осевое сечение усеченного конуса представляет собой равнобедренную трапецию. Основания этой трапеции равны диаметрам оснований конуса, то есть \(2r_б\) и \(2r_м\), где \(r_б\) и \(r_м\) — радиусы большего и меньшего оснований соответственно. Высота трапеции равна высоте конуса \(h\). Площадь трапеции вычисляется по формуле: \(S_{сеч} = \frac{1}{2} (\text{сумма оснований}) \times \text{высота}\). В нашем случае \(S_{сеч} = \frac{1}{2} (2r_б + 2r_м) h = \frac{1}{2} \cdot 2 (r_б + r_м) h = (r_б + r_м) h\).

Площадь боковой поверхности усеченного конуса задается формулой \(S = \pi (r_б + r_м) l\). Из этой формулы мы можем выразить сумму радиусов: \(r_б + r_м = \frac{S}{\pi l}\). Подставляя это выражение в формулу для площади осевого сечения, получаем: \(S_{сеч} = \left(\frac{S}{\pi l}\right) h = \frac{S h}{\pi l}\).

Объем усеченного конуса вычисляется по формуле \(V = \frac{1}{3} \pi h (r_б^2 + r_м^2 + r_б r_м)\). Для использования этой формулы нам необходимо найти значения радиусов \(r_б\) и \(r_м\).

Рассмотрим прямоугольный треугольник, образованный высотой \(h\), образующей \(l\) и отрезком, равным разности радиусов \(r_б — r_м\). По теореме Пифагора для этого треугольника справедливо соотношение: \(h^2 + (r_б — r_м)^2 = l^2\). Отсюда выразим разность радиусов: \(r_б — r_м = \sqrt{l^2 — h^2}\).

Теперь у нас есть система из двух уравнений с двумя неизвестными \(r_б\) и \(r_м\):
1) \(r_б + r_м = \frac{S}{\pi l}\)
2) \(r_б — r_м = \sqrt{l^2 — h^2}\)

Сложим эти два уравнения: \((r_б + r_м) + (r_б — r_м) = \frac{S}{\pi l} + \sqrt{l^2 — h^2}\), что дает \(2r_б = \frac{S}{\pi l} + \sqrt{l^2 — h^2}\). Отсюда находим \(r_б = \frac{1}{2} \left( \frac{S}{\pi l} + \sqrt{l^2 — h^2} \right)\).

Вычтем из первого уравнения второе: \((r_б + r_м) — (r_б — r_м) = \frac{S}{\pi l} — \sqrt{l^2 — h^2}\), что дает \(2r_м = \frac{S}{\pi l} — \sqrt{l^2 — h^2}\). Отсюда находим \(r_м = \frac{1}{2} \left( \frac{S}{\pi l} — \sqrt{l^2 — h^2} \right)\).

Теперь подставим найденные выражения для \(r_б\) и \(r_м\) в формулу объема \(V = \frac{1}{3} \pi h (r_б^2 + r_м^2 + r_б r_м)\).
Сначала упростим выражение в скобках. Заметим, что \(r_б^2 + r_м^2 + r_б r_м = (r_б + r_м)^2 — r_б r_м\).
Мы знаем \(r_б + r_м = \frac{S}{\pi l}\).
Найдем произведение \(r_б r_м\):
\(r_б r_м = \frac{1}{2} \left( \frac{S}{\pi l} + \sqrt{l^2 — h^2} \right) \cdot \frac{1}{2} \left( \frac{S}{\pi l} — \sqrt{l^2 — h^2} \right)\)
\(r_б r_м = \frac{1}{4} \left( \left(\frac{S}{\pi l}\right)^2 — (\sqrt{l^2 — h^2})^2 \right)\)
\(r_б r_м = \frac{1}{4} \left( \frac{S^2}{\pi^2 l^2} — (l^2 — h^2) \right)\)

Теперь подставим выражения для \((r_б + r_м)^2\) и \(r_б r_м\) в \((r_б + r_м)^2 — r_б r_м\):
\(\left(\frac{S}{\pi l}\right)^2 — \frac{1}{4} \left( \frac{S^2}{\pi^2 l^2} — (l^2 — h^2) \right)\)
\( = \frac{S^2}{\pi^2 l^2} — \frac{S^2}{4\pi^2 l^2} + \frac{l^2 — h^2}{4}\)
\( = \frac{4S^2 — S^2}{4\pi^2 l^2} + \frac{l^2 — h^2}{4}\)
\( = \frac{3S^2}{4\pi^2 l^2} + \frac{l^2 — h^2}{4}\)

Теперь подставим это выражение в формулу объема:
\(V = \frac{1}{3} \pi h \left( \frac{3S^2}{4\pi^2 l^2} + \frac{l^2 — h^2}{4} \right)\)
Раскроем скобки:
\(V = \frac{1}{3} \pi h \cdot \frac{3S^2}{4\pi^2 l^2} + \frac{1}{3} \pi h \cdot \frac{l^2 — h^2}{4}\)
\(V = \frac{\pi h S^2}{4\pi^2 l^2} + \frac{\pi h (l^2 — h^2)}{12}\)
Сократим \(\pi\) в первом слагаемом:
\(V = \frac{h S^2}{4\pi l^2} + \frac{\pi h (l^2 — h^2)}{12}\).

Таким образом, площадь осевого сечения усеченного конуса равна \(S_{сеч} = \frac{S h}{\pi l}\), а объем усеченного конуса равен \(V = \frac{h S^2}{4\pi l^2} + \frac{\pi h (l^2 — h^2)}{12}\).