ГДЗ по Геометрии 11 класс Номер 501 Атанасян — Подробные Ответы

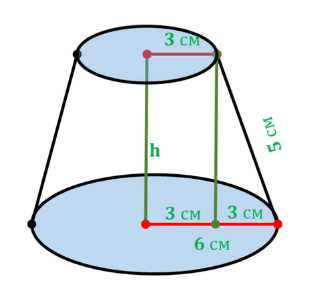
Радиусы оснований усечённого конуса равны 3 м и 6 м, а образующая равна 5 м. Найдите объём усечённого конуса

Дано: меньший радиус основания \(r_м = 3\) м, больший радиус основания \(r_б = 6\) м, образующая \(l = 5\) м.
Найти: объём усечённого конуса \(V\).

Решение:
Объём усечённого конуса находится по формуле \(V = \frac{1}{3} \pi (r_м^2 + r_б^2 + r_м r_б) h\).
Высоту \(h\) найдем из прямоугольного треугольника, образованного высотой, образующей и разностью радиусов оснований, по теореме Пифагора: \(h^2 + (r_б — r_м)^2 = l^2\).
Подставляем значения: \(h^2 + (6 — 3)^2 = 5^2\).
\(h^2 + 3^2 = 5^2\).
\(h^2 + 9 = 25\).
\(h^2 = 25 — 9\).
\(h^2 = 16\).
\(h = 4\) м.
Теперь подставим значения радиусов и высоты в формулу объёма:
\(V = \frac{1}{3} \pi (3^2 + 6^2 + 3 \cdot 6) \cdot 4\).
\(V = \frac{1}{3} \pi (9 + 36 + 18) \cdot 4\).
\(V = \frac{1}{3} \pi (63) \cdot 4\).
\(V = 21 \pi \cdot 4\).
\(V = 84 \pi\) м³.

Ответ: \(V = 84 \pi\) м³.

Дано: усеченный конус с меньшим радиусом основания \(r_м = 3\) м, большим радиусом основания \(r_б = 6\) м и образующей \(l = 5\) м.
Найти: объём усеченного конуса \(V\).

Решение:
Объём усеченного конуса можно вычислить по формуле \(V = \frac{1}{3} \pi (r_м^2 + r_б^2 + r_м r_б) h\), где \(r_м\) и \(r_б\) — радиусы оснований, а \(h\) — высота конуса.
Для применения этой формулы нам необходимо найти высоту \(h\) усеченного конуса. Рассмотрим осевое сечение усеченного конуса. Оно представляет собой равнобокую трапецию. Если опустить высоту из вершины меньшего основания на плоскость большего основания, мы получим прямоугольный треугольник. Гипотенузой этого треугольника является образующая конуса \(l\), одним катетом — высота конуса \(h\), а другим катетом — разность радиусов оснований \(r_б — r_м\).
По теореме Пифагора для этого прямоугольного треугольника справедливо соотношение: \(h^2 + (r_б — r_м)^2 = l^2\).
Подставим известные значения: \(r_м = 3\) м, \(r_б = 6\) м, \(l = 5\) м.
Получаем уравнение: \(h^2 + (6 — 3)^2 = 5^2\).
Упростим выражение в скобках: \(6 — 3 = 3\).
Уравнение принимает вид: \(h^2 + 3^2 = 5^2\).
Вычислим квадраты: \(3^2 = 9\) и \(5^2 = 25\).
Уравнение становится: \(h^2 + 9 = 25\).
Чтобы найти \(h^2\), вычтем 9 из обеих частей уравнения: \(h^2 = 25 — 9\).
Выполним вычитание: \(h^2 = 16\).
Извлечем квадратный корень, чтобы найти высоту \(h\). Поскольку высота не может быть отрицательной, берем положительный корень: \(h = \sqrt{16}\).
Таким образом, высота усеченного конуса равна \(h = 4\) м.
Теперь, когда у нас есть все необходимые значения (радиусы \(r_м = 3\) м, \(r_б = 6\) м и высота \(h = 4\) м), мы можем подставить их в формулу объёма усеченного конуса:
\(V = \frac{1}{3} \pi (r_м^2 + r_б^2 + r_м r_б) h\).
\(V = \frac{1}{3} \pi (3^2 + 6^2 + 3 \cdot 6) \cdot 4\).
Вычислим квадраты и произведение в скобках: \(3^2 = 9\), \(6^2 = 36\), \(3 \cdot 6 = 18\).
Подставим эти значения обратно в формулу: \(V = \frac{1}{3} \pi (9 + 36 + 18) \cdot 4\).
Сложим числа в скобках: \(9 + 36 + 18 = 63\).
Формула принимает вид: \(V = \frac{1}{3} \pi (63) \cdot 4\).
Умножим \(\frac{1}{3}\) на 63: \(\frac{1}{3} \cdot 63 = 21\).
Теперь у нас есть: \(V = 21 \pi \cdot 4\).
Выполним последнее умножение: \(21 \cdot 4 = 84\).
Следовательно, объём усеченного конуса равен \(V = 84 \pi\) м³.

Ответ: Объём усеченного конуса составляет \(84 \pi\) м³.