Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 499 Атанасян — Подробные Ответы
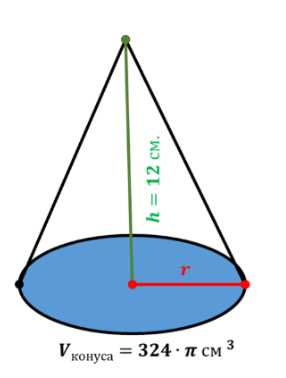
Высота конуса равна 12 см, а его объём равен \(324\pi\) см\(^3\). Найдите угол сектора, который получится, если боковую поверхность конуса развернуть на плоскость.
Дано: высота конуса \(h = 12\) см, объём конуса \(V = 324\pi\) см\(^3\). Найти угол развертки конуса \(\phi\).
Объём конуса выражается формулой \(V = \frac{1}{3} \pi r^2 h\), где \(r\) — радиус основания. Подставим известные значения: \(324\pi = \frac{1}{3} \pi r^2 (12)\), что упрощается до \(324 = 4r^2\). Из этого находим радиус основания: \(r^2 = \frac{324}{4} = 81\), следовательно, \(r = \sqrt{81} = 9\) см (так как радиус положителен).
Образующая конуса \(l\) связана с высотой \(h\) и радиусом основания \(r\) по теореме Пифагора: \(l^2 = h^2 + r^2\). Подставим значения \(h = 12\) и \(r = 9\): \(l^2 = 12^2 + 9^2 = 144 + 81 = 225\). Таким образом, образующая \(l = \sqrt{225} = 15\) см (так как образующая положительна).
Угол сектора развертки боковой поверхности конуса \(\phi\) вычисляется по формуле \(\phi = \frac{360^\circ \cdot r}{l}\). Подставим значения \(r = 9\) и \(l = 15\): \(\phi = \frac{360^\circ \cdot 9}{15} = \frac{360^\circ}{15} \cdot 9 = 24^\circ \cdot 9 = 216^\circ\).
Ответ: угол развертки конуса равен \(216^\circ\).
Дано: высота конуса \(h = 12\) см, объём конуса \(V = 324\pi\) см\(^3\). Необходимо найти угол развертки боковой поверхности конуса \(\phi\).
Первым шагом мы используем формулу для объёма конуса, чтобы найти радиус его основания. Формула объёма конуса имеет вид \(V = \frac{1}{3} \pi r^2 h\), где \(V\) — объём, \(r\) — радиус основания, а \(h\) — высота конуса.
Подставим в эту формулу известные значения объёма \(V = 324\pi\) см\(^3\) и высоты \(h = 12\) см:
\(324\pi = \frac{1}{3} \pi r^2 (12)\).
Мы можем сократить \(\pi\) с обеих сторон уравнения:
\(324 = \frac{1}{3} r^2 (12)\).
Умножим \(\frac{1}{3}\) на 12:
\(324 = 4 r^2\).
Теперь выразим \(r^2\), разделив обе части уравнения на 4:
\(r^2 = \frac{324}{4}\).
Вычислим значение:
\(r^2 = 81\).
Чтобы найти радиус \(r\), извлечем квадратный корень из обеих частей уравнения. Поскольку радиус не может быть отрицательным, мы берем положительный корень:
\(r = \sqrt{81} = 9\) см.
Итак, радиус основания конуса равен 9 см.
Вторым шагом мы найдем образующую конуса \(l\). Образующая, высота и радиус основания конуса образуют прямоугольный треугольник, где образующая является гипотенузой, а высота и радиус — катетами. Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов: \(l^2 = h^2 + r^2\).
Подставим в эту формулу известные значения высоты \(h = 12\) см и найденного радиуса \(r = 9\) см:
\(l^2 = 12^2 + 9^2\).
Вычислим квадраты:
\(l^2 = 144 + 81\).
Сложим значения:
\(l^2 = 225\).
Чтобы найти образующую \(l\), извлечем квадратный корень из обеих частей уравнения. Поскольку образующая не может быть отрицательной, мы берем положительный корень:
\(l = \sqrt{225} = 15\) см.
Итак, образующая конуса равна 15 см.
Третьим шагом мы вычислим угол развертки боковой поверхности конуса. Когда боковая поверхность конуса разворачивается на плоскость, она образует круговой сектор. Радиус этого сектора равен образующей конуса \(l\), а длина дуги сектора равна длине окружности основания конуса \(C = 2\pi r\). Угол сектора \(\phi\) (в градусах) связан с радиусом основания \(r\) и образующей \(l\) формулой:
\(\phi = \frac{360^\circ \cdot r}{l}\).
Подставим в эту формулу найденные значения радиуса \(r = 9\) см и образующей \(l = 15\) см:
\(\phi = \frac{360^\circ \cdot 9}{15}\).
Выполним вычисления:
\(\phi = \frac{3240^\circ}{15}\).
Разделим 3240 на 15:
\(\phi = 216^\circ\).
Таким образом, угол развертки боковой поверхности конуса составляет 216 градусов.
Ответ: угол развертки конуса равен \(216^\circ\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.