Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 498 Атанасян — Подробные Ответы
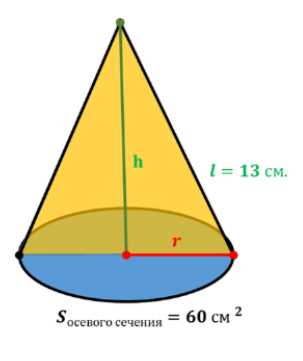
Найдите объём конуса, если его образующая равна 13 см, а площадь осевого сечения равна 60 см\(^2\).
Дано: образующая конуса \(l = 13\) см, площадь осевого сечения \(S_{сеч} = 60\) см\(^2\). Найти: объём конуса \(V_{конуса}\).
Площадь осевого сечения конуса равна \(S_{сеч} = r h\), где \(r\) — радиус основания, \(h\) — высота. По условию \(r h = 60\), откуда \(h = \frac{60}{r}\). По теореме Пифагора для конуса \(r^2 + h^2 = l^2\). Подставим известные значения: \(r^2 + (\frac{60}{r})^2 = 13^2\), что дает \(r^2 + \frac{3600}{r^2} = 169\). Умножим на \(r^2\) (при условии \(r \neq 0\)): \(r^4 + 3600 = 169r^2\), или \(r^4 — 169r^2 + 3600 = 0\). Сделаем замену \(t = r^2\), получим квадратное уравнение \(t^2 — 169t + 3600 = 0\). Дискриминант \(D = (-169)^2 — 4(1)(3600) = 28561 — 14400 = 14161 = 119^2\). Корни уравнения для \(t\): \(t_1 = \frac{169 + 119}{2} = \frac{288}{2} = 144\) и \(t_2 = \frac{169 — 119}{2} = \frac{50}{2} = 25\). Так как \(t = r^2\), то \(r^2 = 144\) или \(r^2 = 25\). Поскольку радиус положителен, \(r_1 = \sqrt{144} = 12\) см или \(r_2 = \sqrt{25} = 5\) см. Найдем соответствующие высоты: если \(r_1 = 12\), то \(h_1 = \frac{60}{12} = 5\) см; если \(r_2 = 5\), то \(h_2 = \frac{60}{5} = 12\) см. Объём конуса вычисляется по формуле \(V = \frac{1}{3} \pi r^2 h\). Для первого случая \(r=12, h=5\): \(V_1 = \frac{1}{3} \pi (12^2)(5) = \frac{1}{3} \pi (144)(5) = 240 \pi\) см\(^3\). Для второго случая \(r=5, h=12\): \(V_2 = \frac{1}{3} \pi (5^2)(12) = \frac{1}{3} \pi (25)(12) = 100 \pi\) см\(^3\).
Ответ: \(V_{конуса} = 240 \pi\) см\(^3\) и \(V_{конуса} = 100 \pi\) см\(^3\).
Дано: образующая конуса \(l = 13\) см, площадь осевого сечения конуса \(S_{сеч} = 60\) см\(^2\). Необходимо найти объём конуса \(V_{конуса}\).
Объём конуса вычисляется по формуле \(V_{конуса} = \frac{1}{3} \pi r^2 h\), где \(r\) — радиус основания конуса, а \(h\) — его высота. Обозначим эту формулу как (*).
Осевое сечение конуса представляет собой равнобедренный треугольник с основанием, равным диаметру основания конуса (\(2r\)), и высотой, равной высоте конуса (\(h\)). Площадь этого треугольника равна половине произведения основания на высоту, то есть \(S_{сеч} = \frac{1}{2} (2r) h = r h\). По условию \(S_{сеч} = 60\) см\(^2\), следовательно, \(r h = 60\). Из этого соотношения можно выразить высоту \(h\) через радиус \(r\): \(h = \frac{60}{r}\). Обозначим это соотношение как (**).
Высота конуса, радиус основания и образующая связаны соотношением, следующим из теоремы Пифагора, примененной к прямоугольному треугольнику, образованному высотой, радиусом и образующей: \(h^2 + r^2 = l^2\). Из этого следует, что \(h = \sqrt{l^2 — r^2}\).
Теперь подставим выражение для \(h\) из соотношения (**) в уравнение, полученное из теоремы Пифагора: \(\frac{60}{r} = \sqrt{l^2 — r^2}\). Возведем обе части уравнения в квадрат: \((\frac{60}{r})^2 = (\sqrt{l^2 — r^2})^2\), что дает \(\frac{3600}{r^2} = l^2 — r^2\).
Подставим известное значение образующей \(l = 13\): \(\frac{3600}{r^2} = 13^2 — r^2\), то есть \(\frac{3600}{r^2} = 169 — r^2\). Умножим обе части уравнения на \(r^2\) (при условии, что \(r \neq 0\)): \(3600 = 169r^2 — r^4\). Перенесем все члены в одну сторону, чтобы получить стандартный вид уравнения: \(r^4 — 169r^2 + 3600 = 0\).
Это уравнение является биквадратным. Сделаем замену переменной: пусть \(t = r^2\). Поскольку \(r\) является радиусом, он должен быть положительным, следовательно, \(r^2 = t\) также должно быть положительным (\(t > 0\)). Уравнение принимает вид квадратного уравнения относительно \(t\): \(t^2 — 169t + 3600 = 0\).
Решим это квадратное уравнение, найдя дискриминант \(D\): \(D = (-169)^2 — 4(1)(3600) = 28561 — 14400 = 14161\). Найдем квадратный корень из дискриминанта: \(\sqrt{D} = \sqrt{14161}\). Для вычисления \(\sqrt{14161}\) можно заметить, что число оканчивается на 1, значит, корень должен оканчиваться на 1 или 9. Можно проверить квадраты чисел, близких к \(\sqrt{16900} = 130\). Например, \(120^2 = 14400\), \(119^2 = (120-1)^2 = 14400 — 240 + 1 = 14161\). Таким образом, \(\sqrt{14161} = 119\).
Найдем корни квадратного уравнения для \(t\):
\(t_1 = \frac{-(-169) + \sqrt{D}}{2(1)} = \frac{169 + 119}{2} = \frac{288}{2} = 144\).
\(t_2 = \frac{-(-169) — \sqrt{D}}{2(1)} = \frac{169 — 119}{2} = \frac{50}{2} = 25\).
Оба корня \(t_1 = 144\) и \(t_2 = 25\) положительны, что соответствует условию \(t > 0\). Теперь вернемся к замене \(t = r^2\).
Случай 1: \(r^2 = t_1 = 144\). Поскольку радиус должен быть положительным (\(r > 0\)), \(r_1 = \sqrt{144} = 12\) см.
Найдем соответствующую высоту \(h_1\) из соотношения (**): \(h_1 = \frac{60}{r_1} = \frac{60}{12} = 5\) см. Высота также должна быть положительной (\(h > 0\)), что выполняется.
Случай 2: \(r^2 = t_2 = 25\). Поскольку радиус должен быть положительным (\(r > 0\)), \(r_2 = \sqrt{25} = 5\) см.
Найдем соответствующую высоту \(h_2\) из соотношения (**): \(h_2 = \frac{60}{r_2} = \frac{60}{5} = 12\) см. Высота также должна быть положительной (\(h > 0\)), что выполняется.
Таким образом, у нас есть два возможных варианта для размеров конуса, удовлетворяющих условиям задачи. Теперь вычислим объём конуса для каждого случая, используя формулу (*).
Для Случая 1 (\(r_1 = 12\) см, \(h_1 = 5\) см):
\(V_1 = \frac{1}{3} \pi r_1^2 h_1 = \frac{1}{3} \pi (12)^2 (5) = \frac{1}{3} \pi (144)(5) = \frac{720}{3} \pi = 240 \pi\) см\(^3\).
Для Случая 2 (\(r_2 = 5\) см, \(h_2 = 12\) см):
\(V_2 = \frac{1}{3} \pi r_2^2 h_2 = \frac{1}{3} \pi (5)^2 (12) = \frac{1}{3} \pi (25)(12) = \frac{300}{3} \pi = 100 \pi\) см\(^3\).
Следовательно, существуют два возможных значения для объёма конуса при заданных условиях.
Ответ: объём конуса может быть \(240 \pi\) см\(^3\) или \(100 \pi\) см\(^3\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.