Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 495 Атанасян — Подробные Ответы
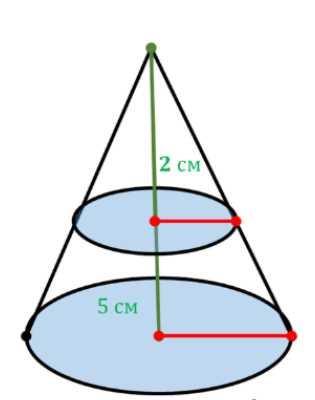
Высота конуса равна 5 см. На расстоянии 2 см от вершины его пересекает плоскость, параллельная основанию. Найдите объём исходного конуса, если объём меньшего конуса, отсекаемого от исходного, равен 24 см\(^3\).
В силу подобия конусов отношение их объемов равно кубу отношения их соответствующих линейных размеров, таких как высоты. Таким образом, мы можем записать соотношение \(\frac{V_{большего}}{V_{меньшего}} = \left(\frac{h_{большего}}{h_{меньшего}}\right)^3\). Известно, что высота меньшего конуса \(h_{меньшего} = 2\) см, высота большего конуса \(h_{большего} = 5\) см, и объем меньшего конуса \(V_{меньшего} = 24\) см\(^3\). Подставляя эти значения в формулу, получаем \(\frac{V_{большего}}{24} = \left(\frac{5}{2}\right)^3\). Вычисляем куб отношения высот: \(\left(\frac{5}{2}\right)^3 = \frac{5^3}{2^3} = \frac{125}{8}\). Теперь уравнение принимает вид \(\frac{V_{большего}}{24} = \frac{125}{8}\). Чтобы найти \(V_{большего}\), умножим обе части уравнения на \(24\): \(V_{большего} = 24 \cdot \frac{125}{8}\). Сокращаем \(24\) и \(8\): \(24 \div 8 = 3\). Получаем \(V_{большего} = 3 \cdot 125\). Произведение \(3\) и \(125\) равно \(375\). Следовательно, объем большего конуса \(V_{большего} = 375\) см\(^3\).
Задача состоит в нахождении объема большего конуса, зная высоту меньшего конуса, высоту большего конуса и объем меньшего конуса. В данном случае мы имеем два подобных конуса. Меньший конус отсечен от большего плоскостью, параллельной основанию большего конуса.
Свойство подобных геометрических тел гласит, что отношение их объемов равно кубу коэффициента подобия. Коэффициент подобия для двух подобных конусов может быть найден как отношение их соответствующих линейных размеров, например, высот или радиусов оснований. В нашем случае нам известны высоты обоих конусов.
Обозначим высоту меньшего конуса как \(h_{меньшего}\), высоту большего конуса как \(h_{большего}\), объем меньшего конуса как \(V_{меньшего}\), и объем большего конуса как \(V_{большего}\). Согласно свойству подобия, отношение объемов этих конусов выражается формулой \(\frac{V_{большего}}{V_{меньшего}} = \left(\frac{h_{большего}}{h_{меньшего}}\right)^3\).
Из условия задачи нам даны следующие значения:
Высота меньшего конуса \(h_{меньшего} = 2\) см.
Высота большего конуса \(h_{большего} = 5\) см.
Объем меньшего конуса \(V_{меньшего} = 24\) см\(^3\).
Нам необходимо найти объем большего конуса \(V_{большего}\). Подставим известные значения в формулу отношения объемов:
\(\frac{V_{большего}}{24} = \left(\frac{5}{2}\right)^3\).
Теперь вычислим значение выражения в правой части уравнения, которое является кубом отношения высот. Чтобы возвести дробь в куб, нужно возвести в куб отдельно числитель и отдельно знаменатель:
\(\left(\frac{5}{2}\right)^3 = \frac{5^3}{2^3}\).
Вычисляем кубы чисел: \(5^3 = 5 \times 5 \times 5 = 125\).
Вычисляем кубы чисел: \(2^3 = 2 \times 2 \times 2 = 8\).
Таким образом, \(\left(\frac{5}{2}\right)^3 = \frac{125}{8}\).
Теперь наше уравнение выглядит так:
\(\frac{V_{большего}}{24} = \frac{125}{8}\).
Чтобы найти \(V_{большего}\), необходимо умножить обе части этого уравнения на \(24\):
\(V_{большего} = 24 \cdot \frac{125}{8}\).
Для удобства вычисления можно сократить \(24\) и \(8\), поскольку \(24\) делится на \(8\): \(24 \div 8 = 3\).
Теперь уравнение упрощается до:
\(V_{большего} = 3 \cdot 125\).
Выполняем умножение: \(3 \times 125 = 375\).
Следовательно, объем большего конуса равен \(375\) см\(^3\).
Ответ: Объем большего конуса равен \(375\) см\(^3\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.