
Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии.
ГДЗ по Геометрии 11 класс Номер 494 Атанасян — Подробные Ответы
Пусть \(h\), \(r\) и \(V\) соответственно высота, радиус основания и объём конуса. Найдите: а) \(V\), если \(h = 3\) см, \(r = 1,5\) см; б) \(h\), если \(r = 4\) см, \(V = 48\pi\) см\(^3\); в) \(r\), если \(h = m\), \(V = p\).
Объём конуса находится по формуле \(V = \frac{1}{3}\pi r^2 h\).
а) При \(h = 3\) см и \(r = 1,5\) см, объём конуса \(V = \frac{1}{3}\pi (1,5)^2 (3) = \frac{1}{3}\pi (2,25)(3) = 2,25\pi\) см\(^3\).
б) При \(r = 4\) см и \(V = 48\pi\) см\(^3\), высота конуса \(h = \frac{3V}{\pi r^2} = \frac{3(48\pi)}{\pi (4)^2} = \frac{144\pi}{16\pi} = 9\) см.
в) При \(h = m\) и \(V = p\), радиус основания конуса \(r = \sqrt{\frac{3V}{\pi h}} = \sqrt{\frac{3p}{\pi m}}\).
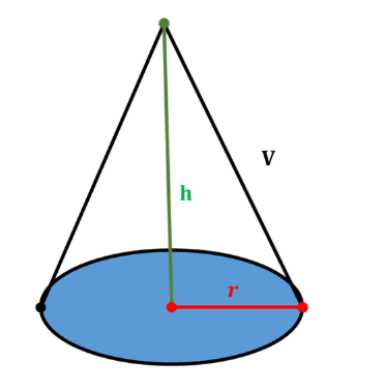
Дано, что \(r\) — радиус основания конуса, \(h\) — высота конуса, а \(V\) — объём конуса. Формула для расчёта объёма конуса имеет вид \(V = \frac{1}{3}\pi r^2 h\). Эта формула связывает объём конуса с радиусом его основания и высотой.
В первом случае, обозначенном как а), требуется найти объём конуса \(V\), когда известны его высота \(h = 3\) см и радиус основания \(r = 1,5\) см. Для этого мы подставим данные значения в формулу объёма конуса \(V = \frac{1}{3}\pi r^2 h\). Подставляя \(r = 1,5\) и \(h = 3\), получаем \(V = \frac{1}{3}\pi (1,5)^2 (3)\). Сначала возведём радиус в квадрат: \((1,5)^2 = 2,25\). Затем умножим полученное значение на высоту и на \(\frac{1}{3}\pi\): \(V = \frac{1}{3}\pi (2,25)(3)\). Умножение \(\frac{1}{3}\) на \(3\) даёт \(1\), поэтому объём равен \(V = \pi (2,25) = 2,25\pi\) см\(^3\). Таким образом, объём конуса в этом случае составляет \(2,25\pi\) кубических сантиметров.
Во втором случае, обозначенном как б), известны радиус основания \(r = 4\) см и объём конуса \(V = 48\pi\) см\(^3\), и требуется найти высоту конуса \(h\). Мы используем ту же формулу объёма конуса \(V = \frac{1}{3}\pi r^2 h\), но на этот раз нам нужно выразить из неё высоту \(h\). Умножим обе части уравнения на \(3\): \(3V = \pi r^2 h\). Теперь разделим обе части на \(\pi r^2\) (при условии, что \(r \neq 0\) и \(\pi \neq 0\)), чтобы получить выражение для \(h\): \(h = \frac{3V}{\pi r^2}\). Подставим известные значения \(V = 48\pi\) и \(r = 4\): \(h = \frac{3(48\pi)}{\pi (4)^2}\). Сначала вычислим квадрат радиуса: \((4)^2 = 16\). Теперь подставим это значение обратно в формулу для \(h\): \(h = \frac{3(48\pi)}{\pi (16)}\). Умножим \(3\) на \(48\pi\) в числителе: \(3 \times 48\pi = 144\pi\). Знаменатель равен \(16\pi\). Теперь разделим числитель на знаменатель: \(h = \frac{144\pi}{16\pi}\). Поскольку \(\pi\) присутствует и в числителе, и в знаменателе, мы можем его сократить (при условии \(\pi \neq 0\)): \(h = \frac{144}{16}\). Деление \(144\) на \(16\) даёт \(9\). Следовательно, высота конуса равна \(h = 9\) см.
В третьем случае, обозначенном как в), даны высота конуса \(h = m\) и объём конуса \(V = p\), и требуется найти радиус основания \(r\). Снова начнём с формулы объёма конуса \(V = \frac{1}{3}\pi r^2 h\). Нам нужно выразить радиус \(r\). Сначала умножим обе части на \(3\): \(3V = \pi r^2 h\). Теперь разделим обе части на \(\pi h\) (при условии, что \(h \neq 0\) и \(\pi \neq 0\)) для получения выражения для \(r^2\): \(r^2 = \frac{3V}{\pi h}\). Чтобы найти \(r\), извлечём квадратный корень из обеих частей уравнения: \(r = \sqrt{\frac{3V}{\pi h}}\). Подставим символьные значения \(V = p\) и \(h = m\): \(r = \sqrt{\frac{3p}{\pi m}}\). Таким образом, радиус основания конуса выражается формулой \(\sqrt{\frac{3p}{\pi m}}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!