Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 493 Атанасян — Подробные Ответы
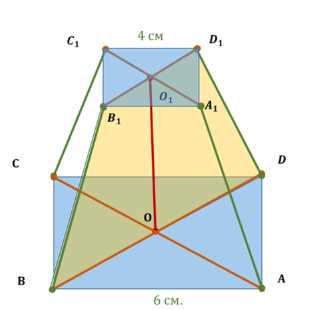
В правильной усечённой четырёхугольной пирамиде стороны оснований равны 6 см и 4 см, а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, равна 15 см\(^2\). Найдите объём усечённой пирамиды.
Дано правильная усечённая четырёхугольная пирамида \(ABCDA_1B_1C_1D_1\). Основания — квадраты со сторонами \(AB = 6\) см и \(A_1B_1 = 4\) см. Площадь сечения \(BDD_1B_1\) равна \(S_{BDD_1B_1} = 15\) см\(^2\). Найти объём \(V_{ABCDA_1B_1C_1D_1}\).
Площади оснований равны \(S_{ABCD} = AB^2 = 6^2 = 36\) см\(^2\) и \(S_{A_1B_1C_1D_1} = A_1B_1^2 = 4^2 = 16\) см\(^2\).
Диагонали оснований равны \(BD = AB\sqrt{2} = 6\sqrt{2}\) см и \(B_1D_1 = A_1B_1\sqrt{2} = 4\sqrt{2}\) см.
Сечение \(BDD_1B_1\) является трапецией с основаниями \(BD\) и \(B_1D_1\) и высотой, равной высоте усечённой пирамиды \(h\).
Площадь трапеции \(S_{BDD_1B_1} = \frac{1}{2}(BD + B_1D_1)h\).
Отсюда найдём высоту \(h\): \(15 = \frac{1}{2}(6\sqrt{2} + 4\sqrt{2})h\), \(15 = \frac{1}{2}(10\sqrt{2})h\), \(15 = 5\sqrt{2}h\), \(h = \frac{15}{5\sqrt{2}} = \frac{3}{\sqrt{2}} = \frac{3\sqrt{2}}{2}\) см.
Объём усечённой пирамиды находится по формуле \(V = \frac{1}{3}h(S_{ABCD} + S_{A_1B_1C_1D_1} + \sqrt{S_{ABCD}S_{A_1B_1C_1D_1}})\).
Подставляем значения: \(V = \frac{1}{3} \cdot \frac{3\sqrt{2}}{2}(36 + 16 + \sqrt{36 \cdot 16})\).
\(V = \frac{\sqrt{2}}{2}(52 + \sqrt{576})\).
\(V = \frac{\sqrt{2}}{2}(52 + 24)\).
\(V = \frac{\sqrt{2}}{2}(76)\).
\(V = 38\sqrt{2}\) см\(^3\).
Ответ: \(38\sqrt{2}\) см\(^3\).
Дано: правильная усечённая четырёхугольная пирамида \(ABCDA_1B_1C_1D_1\). Основаниями являются квадраты. Длина стороны нижнего основания \(AB = 6\) см. Длина стороны верхнего основания \(A_1B_1 = 4\) см. Площадь сечения, проходящего через диагонали \(BD\) и \(B_1D_1\), равна \(S_{BDD_1B_1} = 15\) см\(^2\).
Найти: объём усечённой пирамиды \(V_{ABCDA_1B_1C_1D_1}\).
Первым шагом найдём площади оснований. Поскольку основания являются квадратами, их площади равны квадратам длин их сторон.
Площадь нижнего основания \(S_{ABCD} = AB^2\). Подставляя данное значение \(AB = 6\) см, получаем \(S_{ABCD} = 6^2 = 36\) см\(^2\).
Площадь верхнего основания \(S_{A_1B_1C_1D_1} = A_1B_1^2\). Подставляя данное значение \(A_1B_1 = 4\) см, получаем \(S_{A_1B_1C_1D_1} = 4^2 = 16\) см\(^2\).
Далее найдём длины диагоналей оснований. В квадрате диагональ равна стороне, умноженной на \(\sqrt{2}\).
Длина диагонали нижнего основания \(BD = AB\sqrt{2}\). Подставляя \(AB = 6\) см, получаем \(BD = 6\sqrt{2}\) см.
Длина диагонали верхнего основания \(B_1D_1 = A_1B_1\sqrt{2}\). Подставляя \(A_1B_1 = 4\) см, получаем \(B_1D_1 = 4\sqrt{2}\) см.
Сечение \(BDD_1B_1\) проходит через параллельные диагонали оснований \(BD\) и \(B_1D_1\), и боковые рёбра \(BB_1\) и \(DD_1\). Поскольку основания параллельны, то и диагонали \(BD\) и \(B_1D_1\) параллельны. Следовательно, сечение \(BDD_1B_1\) является трапецией с основаниями \(BD\) и \(B_1D_1\). Высота этой трапеции совпадает с высотой усечённой пирамиды, обозначим её через \(h\).
Площадь трапеции вычисляется по формуле \(S = \frac{1}{2}(\text{сумма оснований}) \times \text{высота}\). Для трапеции \(BDD_1B_1\) это \(S_{BDD_1B_1} = \frac{1}{2}(BD + B_1D_1)h\).
Нам дана площадь \(S_{BDD_1B_1} = 15\) см\(^2\). Подставляем известные значения: \(15 = \frac{1}{2}(6\sqrt{2} + 4\sqrt{2})h\).
Упрощаем выражение в скобках: \(6\sqrt{2} + 4\sqrt{2} = (6+4)\sqrt{2} = 10\sqrt{2}\).
Получаем уравнение: \(15 = \frac{1}{2}(10\sqrt{2})h\).
\(15 = 5\sqrt{2}h\).
Теперь выразим высоту \(h\): \(h = \frac{15}{5\sqrt{2}}\).
Сокращаем дробь: \(h = \frac{3}{\sqrt{2}}\).
Избавляемся от иррациональности в знаменателе, умножив числитель и знаменатель на \(\sqrt{2}\): \(h = \frac{3\sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{3\sqrt{2}}{2}\) см.
Теперь, когда у нас есть площади оснований \(S_{ABCD}\), \(S_{A_1B_1C_1D_1}\) и высота \(h\), мы можем вычислить объём усечённой пирамиды по формуле:
\(V = \frac{1}{3}h(S_{ABCD} + S_{A_1B_1C_1D_1} + \sqrt{S_{ABCD}S_{A_1B_1C_1D_1}})\).
Подставляем найденные значения:
\(V = \frac{1}{3} \cdot \frac{3\sqrt{2}}{2}(36 + 16 + \sqrt{36 \cdot 16})\).
Упрощаем выражение: \(\frac{1}{3} \cdot \frac{3\sqrt{2}}{2} = \frac{\sqrt{2}}{2}\).
Вычисляем сумму площадей оснований: \(36 + 16 = 52\).
Вычисляем произведение площадей оснований под корнем: \(36 \cdot 16 = 576\).
Находим квадратный корень: \(\sqrt{576} = 24\).
Теперь подставляем эти значения обратно в формулу объёма:
\(V = \frac{\sqrt{2}}{2}(52 + 24)\).
Вычисляем сумму в скобках: \(52 + 24 = 76\).
Получаем: \(V = \frac{\sqrt{2}}{2}(76)\).
Умножаем: \(V = \frac{76\sqrt{2}}{2}\).
Сокращаем дробь: \(V = 38\sqrt{2}\) см\(^3\).
Таким образом, объём усечённой пирамиды равен \(38\sqrt{2}\) см\(^3\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.