Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 492 Атанасян — Подробные Ответы
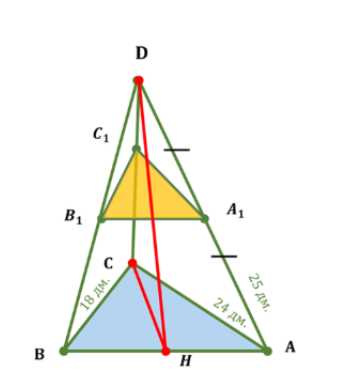
Основанием пирамиды является прямоугольный треугольник, катеты которого равны 24 дм и 18 дм. Каждое боковое ребро равно 25 дм. Пирамида пересечена плоскостью, параллельной плоскости основания и делящей боковое ребро пополам. Найдите объём полученной усечённой пирамиды.
Площадь основания \(\triangle ABC\) находится как половина произведения катетов, поскольку \(\angle ACB = 90^\circ\). \(S_{ABC} = \frac{1}{2} \cdot AC \cdot BC = \frac{1}{2} \cdot 24 \cdot 18 = 216\) дм². Гипотенуза основания \(AB\) по теореме Пифагора равна \(AB = \sqrt{AC^2 + BC^2} = \sqrt{24^2 + 18^2} = \sqrt{576 + 324} = \sqrt{900} = 30\) дм. Поскольку все боковые ребра равны (AD = BD = CD = 25 дм), вершина D проецируется в центр описанной окружности основания. Для прямоугольного треугольника центр описанной окружности находится на середине гипотенузы. Найдем середину гипотенузы AB, назовем ее H. \(AH = BH = \frac{1}{2} AB = \frac{1}{2} \cdot 30 = 15\) дм. В прямоугольном треугольнике ABC, медиана CH к гипотенузе равна половине гипотенузы, так что \(CH = \frac{1}{2} AB = 15\) дм. Таким образом, H является центром описанной окружности, и DH является высотой пирамиды. Найдем высоту DH в прямоугольном треугольнике \(\triangle ADH\) по теореме Пифагора: \(DH = \sqrt{AD^2 — AH^2} = \sqrt{25^2 — 15^2} = \sqrt{625 — 225} = \sqrt{400} = 20\) дм. Объем полной пирамиды ABCD равен \(V_{ABCD} = \frac{1}{3} \cdot S_{ABC} \cdot DH = \frac{1}{3} \cdot 216 \cdot 20 = 72 \cdot 20 = 1440\) дм³. Плоскость сечения \(A_1B_1C_1\) параллельна основанию ABC и делит ребро AD пополам, так как \(AA_1 = A_1D\). Это означает, что пирамида \(A_1B_1C_1D\) подобна пирамиде ABCD с коэффициентом подобия \(\frac{DA_1}{DA} = \frac{1}{2}\). Отношение объемов подобных пирамид равно кубу коэффициента подобия: \(\frac{V_{A_1B_1C_1D}}{V_{ABCD}} = (\frac{1}{2})^3 = \frac{1}{8}\). Следовательно, объем отсеченной пирамиды \(V_{A_1B_1C_1D} = \frac{1}{8} V_{ABCD}\). Объем усеченной пирамиды \(V_{ABCA_1B_1C_1}\) равен разности объемов полной и отсеченной пирамид: \(V_{ABCA_1B_1C_1} = V_{ABCD} — V_{A_1B_1C_1D} = V_{ABCD} — \frac{1}{8} V_{ABCD} = \frac{7}{8} V_{ABCD}\). Подставляя значение объема полной пирамиды, получаем \(V_{ABCA_1B_1C_1} = \frac{7}{8} \cdot 1440 = 7 \cdot 180 = 1260\) дм³.
Дано, что основанием пирамиды ABCD является прямоугольный треугольник \(\triangle ABC\) с прямым углом при вершине C. Длины катетов AC и BC равны 24 дм и 18 дм соответственно. Все боковые ребра пирамиды равны 25 дм, то есть \(AD = BD = CD = 25\) дм. Пирамида пересечена плоскостью \(A_1B_1C_1\), которая параллельна плоскости основания ABC, и при этом ребро AD делится пополам, то есть \(AA_1 = A_1D\). Требуется найти объем усеченной пирамиды \(ABCA_1B_1C_1\).
Первым шагом найдем площадь основания \(\triangle ABC\). Поскольку это прямоугольный треугольник, его площадь равна половине произведения длин катетов: \(S_{ABC} = \frac{1}{2} \cdot AC \cdot BC = \frac{1}{2} \cdot 24 \cdot 18 = 12 \cdot 18 = 216\) дм².
Далее найдем длину гипотенузы AB основания \(\triangle ABC\) по теореме Пифагора: \(AB = \sqrt{AC^2 + BC^2} = \sqrt{24^2 + 18^2} = \sqrt{576 + 324} = \sqrt{900} = 30\) дм.
Поскольку все боковые ребра пирамиды равны, вершина D проецируется в центр описанной окружности основания. Для прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы. Обозначим середину гипотенузы AB как H. Тогда H является центром описанной окружности \(\triangle ABC\), а DH является высотой пирамиды ABCD, перпендикулярной плоскости основания. Радиус описанной окружности равен половине гипотенузы: \(AH = BH = CH = \frac{1}{2} AB = \frac{1}{2} \cdot 30 = 15\) дм.
Теперь найдем высоту DH пирамиды, используя прямоугольный треугольник \(\triangle ADH\). По теореме Пифагора: \(DH = \sqrt{AD^2 — AH^2} = \sqrt{25^2 — 15^2} = \sqrt{625 — 225} = \sqrt{400} = 20\) дм.
Объем полной пирамиды ABCD равен одной трети произведения площади основания на высоту: \(V_{ABCD} = \frac{1}{3} \cdot S_{ABC} \cdot DH = \frac{1}{3} \cdot 216 \cdot 20 = 72 \cdot 20 = 1440\) дм³.
Плоскость сечения \(A_1B_1C_1\) параллельна основанию ABC. Это означает, что малая пирамида \(A_1B_1C_1D\) подобна большой пирамиде ABCD. Поскольку плоскость сечения делит ребро AD пополам (\(AA_1 = A_1D\)), точка \(A_1\) является серединой ребра AD. Следовательно, коэффициент подобия между малой пирамидой \(A_1B_1C_1D\) и большой пирамидой ABCD равен отношению соответствующих линейных размеров, например, \(\frac{DA_1}{DA} = \frac{A_1D}{AD} = \frac{1}{2}\).
Отношение объемов подобных тел равно кубу коэффициента подобия. Поэтому отношение объема малой пирамиды к объему большой пирамиды равно \((\frac{1}{2})^3 = \frac{1}{8}\). Таким образом, \(V_{A_1B_1C_1D} = \frac{1}{8} V_{ABCD}\).
Объем отсеченной малой пирамиды \(A_1B_1C_1D\) равен \(V_{A_1B_1C_1D} = \frac{1}{8} \cdot 1440 = 180\) дм³.
Объем усеченной пирамиды \(ABCA_1B_1C_1\) равен разности объемов полной пирамиды ABCD и отсеченной малой пирамиды \(A_1B_1C_1D\): \(V_{ABCA_1B_1C_1} = V_{ABCD} — V_{A_1B_1C_1D} = 1440 — 180 = 1260\) дм³.
Объем усеченной пирамиды равен 1260 дм³.
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.