Когда речь заходит о школьной геометрии в старших классах, имя Л.С. Атанасяна всплывает одним из первых. Его учебник для 10–11 классов — это не просто набор параграфов и задач, а настоящий проводник, который уже много десятилетий помогает поколениям учеников осваивать непростой, но увлекательный мир стереометрии. Почему же он выдержал испытание временем и остается актуальным?
Этот учебник подкупает своей кристальной ясностью и строгой логикой. Он выстраивает здание стереометрии кирпичик за кирпичиком, начиная с фундаментальных аксиом и постепенно подводя к сложным пространственным конструкциям, векторам и координатному методу. Чувствуется продуманность каждого раздела, а система упражнений в конце глав позволяет не просто закрепить материал, но и по-настоящему погрузиться в тему, решая задачи разного калибра – от базовых до требующих нетривиального подхода.
Одно из главных достоинств пособия — это удивительный баланс между сухой теорией и живой практикой. Каждое определение, каждая теорема сопровождается наглядными, хоть и черно-белыми, чертежами, которые помогают «увидеть» пространственные отношения. Задачи подобраны мастерски: они не только тренируют применение формул, но и развивают то самое «геометрическое зрение», без которого стереометрия остается лишь набором абстракций. Разделы вроде параллельности или перпендикулярности прямых и плоскостей демонстрируют это особенно ярко, предлагая как классические доказательства, так и задачи, над которыми придется поломать голову.
Нельзя не отметить и его роль в подготовке к выпускным экзаменам. Учебник Атанасяна – это отличная база для успешной сдачи ЕГЭ, особенно в части заданий, связанных с построением сечений многогранников и применением координатно-векторного метода. Многие задачи прямо перекликаются с экзаменационным форматом.
Язык изложения, несмотря на строгость предмета, остается удивительно доступным. Даже такие темы, как уравнения плоскости или прямой в пространстве, вводятся постепенно, опираясь на уже усвоенные понятия планиметрии и алгебры. Это создает ощущение непрерывности и логичности учебного процесса. А приятным бонусом в некоторых изданиях служат исторические справки, добавляющие контекст и показывающие, какой долгий путь прошла геометрия от Евклида до наших дней.
Как максимально эффективно работать с этим учебником? Ученикам стоит взять за правило: сначала вдумчиво разобрать примеры, предложенные автором, понять логику решения, а уже потом переходить к самостоятельной работе над задачами. Учителя найдут в нем надежный каркас как для традиционных уроков, так и для более творческих форм работы, например, организации проектов по созданию моделей геометрических тел. Родителям, помогающим своим детям, стоит обратить внимание на «Вопросы для повторения» – это отличный диагностический инструмент для выявления пробелов в знаниях.
Конечно, идеальных учебников не бывает. Кому-то может не хватать ярких цветных иллюстраций, а в редких тиражах встречаются досадные опечатки в ответах (всегда лучше перепроверить с преподавателем!). Но эти мелкие шероховатости ничуть не умаляют его достоинств.
В конечном итоге, учебник Атанасяна — это больше, чем просто источник информации. Это школа мышления. Он учит не просто находить ответы, а выстраивать логические цепочки, видеть пространственные связи и анализировать условия задачи. Это навык, который пригодится далеко за пределами школьного курса геометрии.
ГДЗ по Геометрии 11 класс Номер 491 Атанасян — Подробные Ответы
Основания усечённой пирамиды — равнобедренные прямоугольные треугольники, гипотенузы которых равны \(m\) и \(n\) (\(m > n\)). Две боковые грани, содержащие катеты, перпендикулярны к основанию, а третья составляет с ним угол \(\phi\). Найдите объём усечённой пирамиды.
Объем усеченной пирамиды находится как разность объемов полной пирамиды и отсеченной верхней пирамиды. Объем пирамиды равен \(V = \frac{1}{3} S_{основания} \cdot h\).
Достроим усеченную пирамиду до полной пирамиды ABCD. Поскольку грани BCD и ABD перпендикулярны основанию ABC, высота пирамиды ABCD есть ребро BD. Объем полной пирамиды ABCD равен \(V_{ABCD} = \frac{m^3}{24} tg(\phi)\). Объем отсеченной пирамиды A₁B₁C₁D по аналогии равен \(V_{A_1B_1C_1D} = \frac{n^3}{24} tg(\phi)\). Тогда объем усеченной пирамиды ABCA₁B₁C₁ равен \(V_{ABCA_1B_1C_1} = V_{ABCD} — V_{A_1B_1C_1D} = \frac{m^3}{24} tg(\phi) — \frac{n^3}{24} tg(\phi) = \frac{m^3 — n^3}{24} tg(\phi)\). Ответ: \(V_{ABCA_1B_1C_1} = \frac{m^3 — n^3}{24} tg(\phi)\).
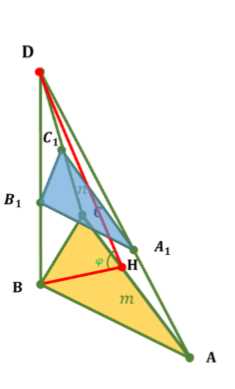
Объем усеченной пирамиды может быть найден как разность объемов полной пирамиды, из которой она получена, и объема меньшей подобной пирамиды, которая была отсечена сверху. В данном случае, усеченная пирамида \(ABCA_1B_1C_1\) является частью полной пирамиды ABCD с вершиной D. Основания усеченной пирамиды, \(\triangle ABC\) и \(\triangle A_1B_1C_1\), являются равнобедренными прямоугольными треугольниками. Гипотенуза нижнего основания \(\triangle ABC\) равна \(AC = m\), а гипотенуза верхнего основания \(\triangle A_1B_1C_1\) равна \(A_1C_1 = n\).
Поскольку две боковые грани, содержащие катеты (\(\triangle DBC\) и \(\triangle DAB\)), перпендикулярны к плоскости основания ABC, их линия пересечения BD перпендикулярна плоскости основания ABC. Следовательно, BD является высотой полной пирамиды ABCD.
Рассмотрим нижнее основание \(\triangle ABC\). Это равнобедренный прямоугольный треугольник с гипотенузой \(AC = m\). Катеты AB и BC равны. По теореме Пифагора \(AB^2 + BC^2 = AC^2\), что дает \(2 AB^2 = m^2\), откуда \(AB = BC = \frac{m}{\sqrt{2}}\). Площадь основания \(\triangle ABC\) равна \(S_{ABC} = \frac{1}{2} \cdot AB \cdot BC = \frac{1}{2} \cdot \frac{m}{\sqrt{2}} \cdot \frac{m}{\sqrt{2}} = \frac{1}{2} \cdot \frac{m^2}{2} = \frac{m^2}{4}\). Высота BH в равнобедренном прямоугольном треугольнике, опущенная на гипотенузу AC, делит ее пополам и равна половине гипотенузы, то есть \(BH = \frac{1}{2} AC = \frac{m}{2}\).
Угол \(\phi\) задан как \(\angle DACB = \phi\), но на рисунке он показан как угол между ребром DB и отрезком BH, то есть \(\angle DBH = \phi\). Предполагая, что \(\phi\) — это угол между боковой гранью ADC и основанием ABC, и что BH является проекцией DH на основание, тогда в прямоугольном треугольнике DBH, где BD перпендикулярно основанию, \(tg(\phi) = \frac{BD}{BH}\). Отсюда высота пирамиды \(BD = BH \cdot tg(\phi)\). Подставляя значение \(BH = \frac{m}{2}\), получаем \(BD = \frac{m}{2} tg(\phi)\).
Объем полной пирамиды ABCD равен \(V_{ABCD} = \frac{1}{3} \cdot S_{ABC} \cdot BD = \frac{1}{3} \cdot \frac{m^2}{4} \cdot \frac{m}{2} tg(\phi) = \frac{m^3}{24} tg(\phi)\).
Верхнее основание \(\triangle A_1B_1C_1\) подобно нижнему основанию \(\triangle ABC\), с коэффициентом подобия, равным отношению гипотенуз \(\frac{n}{m}\). Пирамида \(A_1B_1C_1D\) подобна пирамиде ABCD. Отношение линейных размеров подобных пирамид равно коэффициенту подобия оснований, то есть \(\frac{n}{m}\). Отношение объемов подобных тел равно кубу коэффициента подобия. Однако, здесь удобнее рассмотреть пирамиду \(A_1B_1C_1D\) с вершиной D и основанием \(A_1B_1C_1\). Высота этой пирамиды, опущенная из D на плоскость \(A_1B_1C_1\), является частью высоты BD полной пирамиды. По аналогии с расчетом объема полной пирамиды, объем пирамиды \(A_1B_1C_1D\) с основанием, имеющим гипотенузу \(n\), может быть записан как \(V_{A_1B_1C_1D} = \frac{n^3}{24} tg(\phi)\).
Объем усеченной пирамиды \(ABCA_1B_1C_1\) равен разности объемов полной пирамиды ABCD и отсеченной пирамиды \(A_1B_1C_1D\): \(V_{ABCA_1B_1C_1} = V_{ABCD} — V_{A_1B_1C_1D} = \frac{m^3}{24} tg(\phi) — \frac{n^3}{24} tg(\phi) = \frac{m^3 — n^3}{24} tg(\phi)\).
Таким образом, объем усеченной пирамиды равен \(\frac{m^3 — n^3}{24} tg(\phi)\).
Исследовательские задачи
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.